Abstract
Normalerweise verwenden Sie Bereichsnamen in Excel, um eine hartkodierte Zuweisung zu Eingabe- oder Ausgabezellen zu vermeiden. Wenn Sie wichtigen Zellen Namen zuweisen, werden deren Bezüge bei Zeilen- oder Spalteneinfügungen oder -löschungen automatisch angepasst.
Hier wollen wir Bereichsnamen in Excel für die effiziente Implementierung einer einfachen Lösung mit verschachtelten Tabellenblattfunktionen verwenden, die nicht mehr verändert werden muss:
Für eine (fast) beliebige Anzahl von Spielern wollen wir ein einfaches Rundenturnier organisieren, bei dem jeder Spieler gegen jeden anderen genau einmal spielt. Der Einfachheit halber legen wir fest, dass Spieler 1 im ersten Spiel Heimrecht haben soll (oder anders ausgedrückt: mit Weiß spielt).
Wir können nun einfache verschachtelte Formeln mit Bereichsnamen realisieren. Dabei sind die notwendigen Parameter die jeweiligen Zeilen- und Spaltenpositionen relativ zum Ankerpunkt der Paarungstabelle oben links.
Bitte beachten Sie: Ein Bereichsname wird genau dann ausgewertet, wenn eine Formel berechnet wird, die sich auf ihn bezieht. Dies bedeutet, dass er mehrfach ausgewertet wird, wenn er in mehreren neuberechneten Formeln genutzt wird. Unrefenzierte Bereichsnamen werden nicht ausgewertet, auch nicht bei einer vollständigen Neuberechnung (STRG + ALT + F9).
Entwickeln einer Formellösung für ein Rundenturnier Jeder gegen Jeden
Für unser einfaches Rundenturnier haben wir nach Festlegung der Turnierart lediglich einen Parameter, die Anzahl der Spieler.
Wir wollen die zu spielenden Paarungen in einer einfachen Tabelle ausgeben. Beispiel:
| Tisch 1 | Tisch 2 | Tisch 3 | |
|---|---|---|---|
| Runde 1 | 1 - 6 | 5 - 2 | 3 - 4 |
| Runde 2 | 5 - 1 | 4 - 6 | 2 - 3 |
| Runde 3 | 1 - 4 | 3 - 5 | 6 - 2 |
| Runde 4 | 3 - 1 | 2 - 4 | 5 - 6 |
| Runde 5 | 1 - 2 | 6 - 3 | 4 - 5 |
Die Paarungen je Runde zeigen wir in den Zeilen, an welchem Tisch (oder Platz) gespielt werden soll, steht in den Spalten, und der jeweils erstgenannte Spieler hat Heimrecht (spielt mit Weiß).
Der Name des Tabellenblattes, in dem unsere Eingabe (Spieleranzahl) und Ausgaben (die Paarungstabelle) stehen, soll Eingabe_und_Ausgabe lauten.
Die Eingabezelle für die Spieleranzahl nennen wir Player_Count. Sie hat den Wert =Eingabe_und_Ausgabe!$B$1.
Damit die Paarungstabelle einfach verschoben werden kann, legen wir als Anker den Namen Table_Top_Left (hier mit dem Wert =Eingabe_und_Ausgabe!$A$10) fest. Die weiteren Bereichsnamen legen wir relativ zu diesem Anker fest, um absolute Bezüge zu vermeiden.
Der aktuelle Tisch (Spalte) soll This_Table heißen mit dem Wert =SPALTE() - SPALTE(Table_Top_Left). Die aktuelle Runde (Zeile) soll This_Round heißen mit dem Wert =ZEILE() - ZEILE(Table_Top_Left).
Die Spaltenköpfe (Tisch 1, Tisch 2, …) können wir dann einfach Table_Title mit dem Wert =WENN(ISTGERADE(Player_Count); WENN(This_Table <= Player_Count / 2; “Tisch " & This_Table; “"); WENN(This_Table = 1; “Frei”; WENN(This_Table <= (Player_Count + 1) / 2; “Tisch " & This_Table - 1; “"))) nennen. Die Zeilenköpfe (Runde 1, Runde 2, …) heißen Round_Title mit dem Wert =WENN(This_Round <= (Player_Count - WENN(ISTUNGERADE(Player_Count); 0; 1)); “Runde " & This_Round; “").
Schließlich legen wir für die jeweiligen Paarungen den allgemeinen Namen This_Game mit dem Wert =WENN(UND(This_Round <= (Player_Count - WENN(ISTUNGERADE(Player_Count); 0; 1)); This_Table <= (Player_Count + 1) / 2); WENN(ISTGERADE(Player_Count); Even_This_Game; Odd_This_Game); “") fest.
Anmerkung: Die weiter notwendigen Namen Even_This_Game und Odd_This_Game erklären wir in den unten gezeigten Kapiteln für eine gerade bzw. ungerade Spieleranzahl.
Nun ist die Festlegung der auszugebenden Paarungstabelle einfach: In die erste Zeile geben wir in die zweite Spalte Table_Title ein. In die erste Spalte geben wir in die zweite Zeile Round_Title ein. Die erste Paarung in der zweiten Zeile und zweiten Spalte lautet einfach: This_Game. Wir kopieren die letzte Spalte nach rechts und die unterste Zeile nach unten, bis wir leere Zellen als Ausgabe erhalten.
Beispiel für eine gerade Spieleranzahl
Das Bildungsgesetz für die Paarungen bei gerader Spieleranzahl: Wir sehen an der obigen Beispieltabelle für 6 Spieler, dass Spieler 1 immer an Tisch 1 sitzen bleibt und gegen die Spieler 6, 5, 4, … mit wechselnden Farben beginnend mit Weiß spielt. In der ersten Runde spielen der erste Spieler gegen den letzten, der zweite gegen den vorletzten, usw., aber immer mit wechselnden Farben. In den folgenden Runden wird an den Tischen größer 1 jeder Spieler durch den nächstniedrigeren (in der Formel zu erkennen an dem Summanden - This_Round) ersetzt. Ausnahme: Auf Spieler 2 folgt der letzte Spieler (hier 6).
Damit wird die Festlegung der folgenden Namen klar:
| Name | Bezieht sich auf |
|---|---|
| Even_Equal_One_PlayerA | =1 |
| Even_Equal_One_PlayerB | =(1 + Player_Count - This_Round) |
| Even_Greater_One_PlayerA | =(2 + REST(Player_Count - This_Table - This_Round; Player_Count - 1)) |
| Even_Greater_One_PlayerB | =(2 + REST(This_Table - This_Round - 1; Player_Count - 1)) |
| Even_This_Game | =WENN(This_Table = 1; WENN(ISTUNGERADE(This_Round); Even_Equal_One_PlayerA & " - " & Even_Equal_One_PlayerB; Even_Equal_One_PlayerB & " - " & Even_Equal_One_PlayerA); WENN(ISTGERADE(This_Table); Even_Greater_One_PlayerA & " - " & Even_Greater_One_PlayerB; Even_Greater_One_PlayerB & " - " & Even_Greater_One_PlayerA)) |
Beispiel für eine ungerade Spieleranzahl
| Frei | Tisch 1 | Tisch 2 | Tisch 3 | |
|---|---|---|---|---|
| Runde 1 | 7 pausiert | 1 - 6 | 5 - 2 | 3 - 4 |
| Runde 2 | 6 pausiert | 7 - 5 | 4 - 1 | 2 - 3 |
| Runde 3 | 5 pausiert | 6 - 4 | 3 - 7 | 1 - 2 |
| Runde 4 | 4 pausiert | 5 - 3 | 2 - 6 | 7 - 1 |
| Runde 5 | 3 pausiert | 4 - 2 | 1 - 5 | 6 - 7 |
| Runde 6 | 2 pausiert | 3 - 1 | 7 - 4 | 5 - 6 |
| Runde 7 | 1 pausiert | 2 - 7 | 6 - 3 | 4 - 5 |
Das Bildungsgesetz für die Paarungen bei ungerader Spieleranzahl: In der ersten Runde pausiert der letzte Spieler, in der zweiten der vorletzte, usw. In der ersten Runde spielen der erste Spieler gegen den vorletzten, der zweite gegen den vorvorletzten, usw., aber immer mit wechselnden Farben. In den folgenden Runden wird an den Tischen größer 1 jeder Spieler durch den nächstniedrigeren (in der Formel zu erkennen an dem Summanden - This_Round) und Spieler 1 durch den Letzten ersetzt.
Damit wird auch die Festlegung der folgenden Namen klar:
| Name | Bezieht sich auf |
|---|---|
| Odd_Equal_One_PlayerA | =(Player_Count - This_Round + 1) |
| Odd_Greater_One_PlayerA | =(1 + REST(This_Table - This_Round - 1; Player_Count)) |
| Odd_Greater_One_PlayerB | =(1 + REST(Player_Count - This_Table - This_Round + 1; Player_Count)) |
| Odd_This_Game | =WENN(This_Table = 1; Odd_Equal_One_PlayerA & " pausiert”; WENN(ISTGERADE(This_Table); Odd_Greater_One_PlayerA & " - " & Odd_Greater_One_PlayerB; Odd_Greater_One_PlayerB & " - " & Odd_Greater_One_PlayerA)) |
Eine kleine Quizfrage: Warum existiert der Name Odd_Equal_One_PlayerB nicht?
Antwort: Weil die Formeln als Tisch 1 den pausierenden Spieler ansehen und die Tischnummern bei ungerader Spieleranzahl künstlich um 1 reduziert werden - siehe die Formel von Table_Title.
Noch eine kleine Quizfrage: Wie kann man diese Lösung erweitern, um die Paarungen for mehrere verschiedene Turniere in einer Excel-Datei zu berechnen?
Antwort: Erstellen Sie alle genannten Bereichsnamen als lokale Namen im aktuellen Tabellenblatt und kopieren Sie dann das Tabellenblatt so oft wie nötig. Leider können Sie nicht lediglich die Namen Player_Count und Table_Top_Left lokal definieren. Alle Bereichsnamen müssen so häufig existieren wie sie Turniere berechnen wollen.
Appendix – Die Excel Datei für ein einfaches Rundenturnier Jeder gegen Jeden
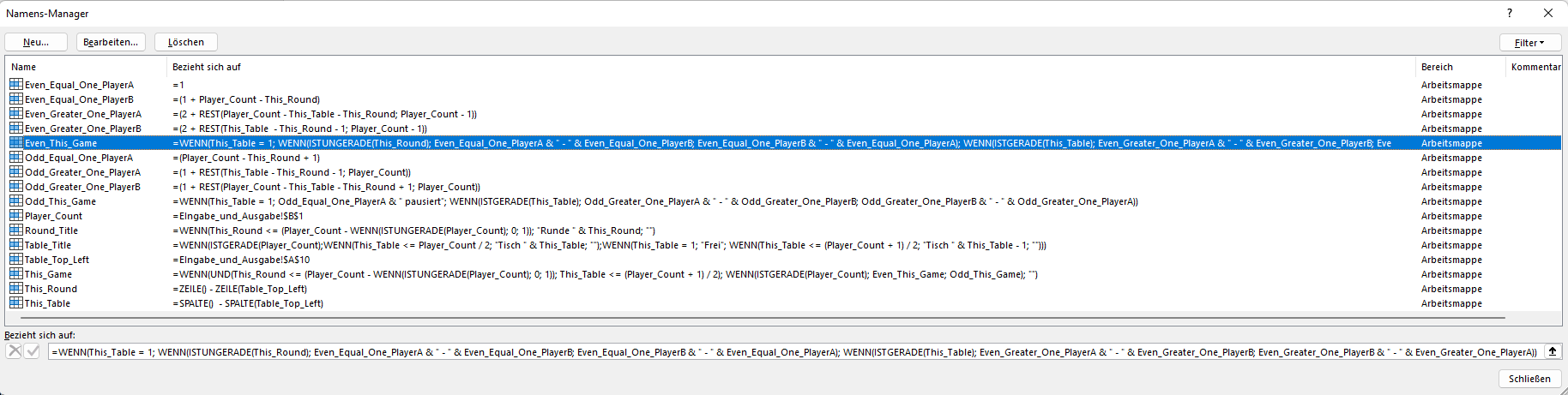
Das Interessante ist: Sie können auch diesen Ansatz für (fast) beliebig viele Spieler verwenden. Kopieren Sie lediglich die Zeilen so weit wie nötig nach unten und die Spalten nach rechts, bis Sie Leerzellen erhalten.
Die Formeln funktionieren sogar für die pathologischen Fälle mit keinem, einem oder zwei Spielern.
Download
Bitte den Haftungsausschluss im Impressum beachten.
Rundenturnier.xlsx [20 KB Excel Datei, ohne jegliche Gewährleistung]
Anmerkung: Eine allgemeinere Lösung für Rundenturniere, bei der Sie auch die Farbe für Spieler 1 in der ersten Runde frei wählen können, und die eine zusätzliche Ausgabematrix erzeugt, finden Sie unter sbRoundRobin.