Exakte Rechnung mit Rationalen Zahlen ·

Abstract

Vorgestellt wird die Möglichkeit der genauen Rechnung mit rationalen Zahlen. Die Vorteile einer Rationalzahlarithmetik gegenüber einer Festpunkt- oder Gleitpunktarithmetik:

Die Möglichkeit der genauen Darstellung aller “einfachen” Brüche (wie 1/3, 3/7 usw.).
Die Möglichkeit der Berechnung genauer Zwischenergebnisse bei den Grundrechenarten (einschließlich der Division!).
Die Existenz des genauen multiplikativen Inversen aller Elemente (außer 0) im darzustellenden Bereich.
Bei festem Bruchstrich (engl. fixed slash) Unabhängigkeit von der Zahlenbasis.

Rationalzahlen in Rechenanlagen

Fixed Slash

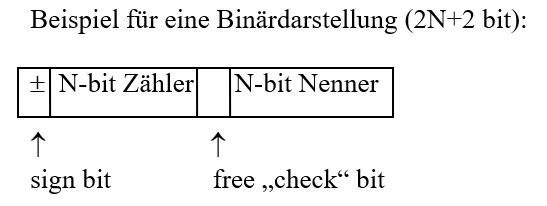
Für Zähler und Nenner stehen jeweils die gleiche Anzahl von Stellen zur Verfügung: Rationalzahlen_Fixed_Slash

Floating Slash

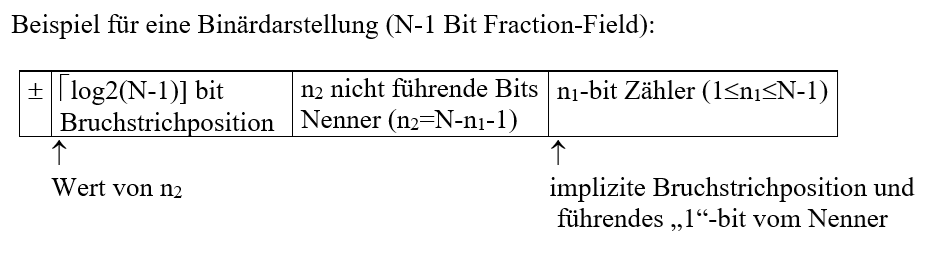
Die Summe der Stellen für Zähler und Nenner ist fest: Rationalzahlen_Floating_Slash

Die Definition der Grundrechenarten

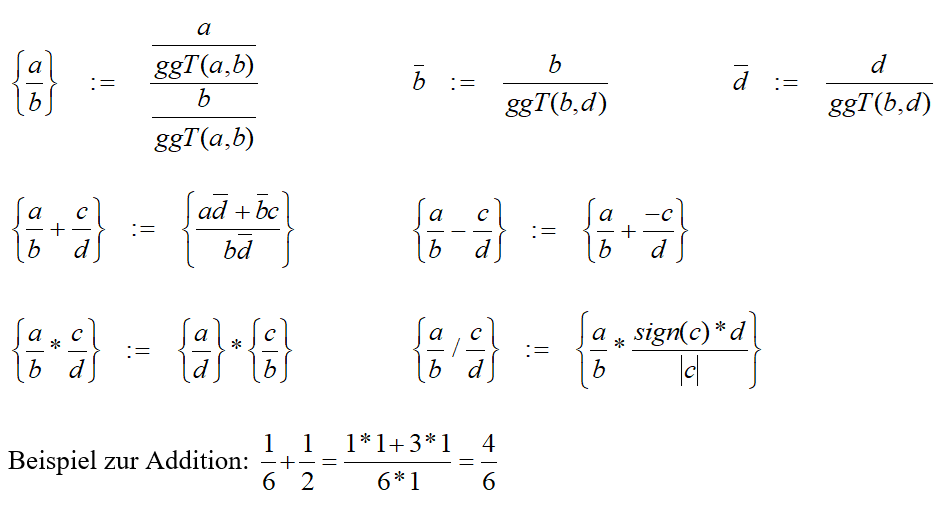
Seien a, c ganze Zahlen und b, d natürliche Zahlen. Rationalzahlen_Grundrechenarten

Der größte gemeinsame Teiler

Flowchart

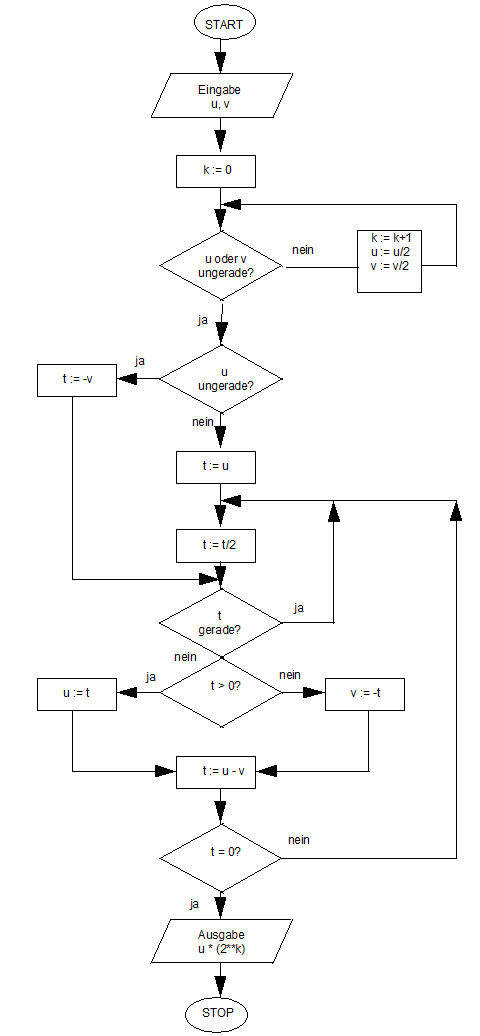
Rationalzahlen_GGT_Flowchart

Z-80 Assemblerprogramm

100   ; ################################
110   ; # GROESSTER GEMEINSAMER TEILER #
120   ; ################################
130   *MLIST OFF
140   ; BINAERER GGT-ALGORITHMUS (1967 VON JOSEF STEIN)
150   ;
160   ; BERECHNUNG DES GGT'S ZWEIER NATUERLICHER ZAHLEN U
170   ; UND V
180   ; REGISTERPAAR ZEIGER AUF LOWEST-SIGNIFICANT-BYTE VON
190   ;      HL           U
200   ;      DE           V
210   ;      BC           T
220   ; DAS PROGRAMM BENUTZT DIE REGISTER AF,BC,DE,HL,IX,IY,SP
230   ; DER GGT(U,V) STEHT SCHLIESSLICH IN U (VON HL ANGEZEIGT)
240   ;
250   LAENGE EQU 12 ; LAENGE DER INTEGER-DARSTELLUNG
260   LANG EQU LAENGE-15 LAENGE DER DARSTELLUNG - l
270   ; ##########################
280   ; # DIE MACRO-DEFINITIONEN #
290   ; ##########################
300   ;
310   ; BILDUNG DES ZWEIER-KOMPLEMENTES
320   ;
330   COM MACRO #PAR
340   PUSH BC
350   PUSH #PAR ; PARAMETER-UEBERGABE
360   POP IX
370   LD B,LAENGE
380   A#SYM LD A,(IX-LANG); BILDUNG DES EINERKOMPLEMENTES
390   XOR 0FFH
400   LD (IX-LANG),A
410   INC IX
420   DJNZ A#SYM
430   DEC IX
440   LD B,LAENGE
450   B#SYM INC (IX-LANG); UND EINS ADDIEREN
460   JR NZ,C#SYM; KEIN UEBERTRAG: FERTIG!
470   DEC IX
480   DJNZ B#SYM
490   C#SYM POP BC
500   ENDM
510   ;
520   ; WERTZUWEISUNG
530   ;
540   LOAD MACRO #PAR1,#PAR2
550   PUSH BC
560   PUSH HL
570   PUSH DE
580   PUSH #PAR1 ; PARAMETER-UEBERGABE
590   PUSH #PAR2
600   POP HL
610   POP DE
620   LD BC,LAENGE
630   LDDR
640   POP DE
650   POP HL
660   POP BC
670   ENDM