Gewichtberechnung (Excel / VBA) ·

Abstract

Angenommen, Sie haben drei verschiedene Produkte in jeweils 3 Ausprägungen mit unterschiedlichen Gewichten, die auch in unterschiedlicher Anzahl vorliegen. Das Produkt PR existiert mit den Gewichten 404 g (davon gibt es 7 Stück), 401 g (vier Mal) und 398 g (fünf Mal), und es gibt entsprechend weitere Produkte BB und BO:

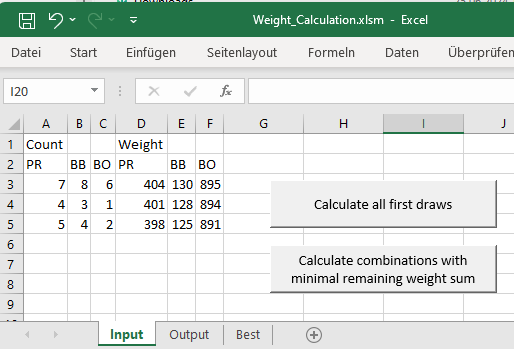
weight_calculation_input

Nun sollen jeweils drei mal drei Produkte (immer von allen drei Produkten genau eins) mit identischer Gewichtssumme ermittelt und die Restmenge an Produkten ausgegeben werden:

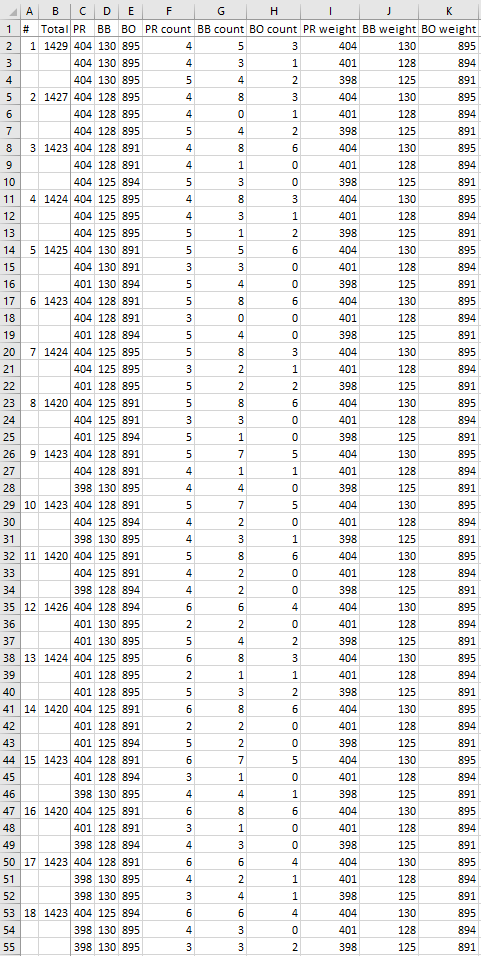
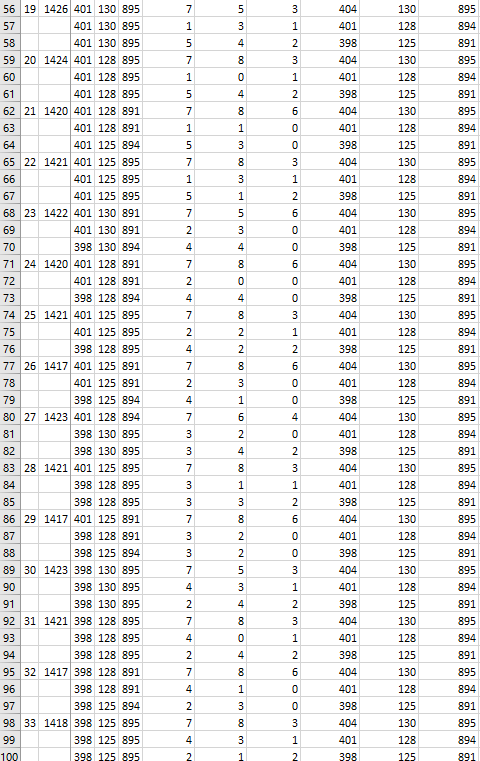
weight_calculation_output1 weight_calculation_output2

Es gibt viele Alternativen, alle möglichen Entnahmen zu ermitteln. Im Anhang ist eine sehr einfache, aber recht aufwendige Option genannt (siehe erste Download Datei), die naiv alle möglichen Kombinationen durchgeht. Die zweite Download Datei zeigt eine Monte Carlo Simulation, die die Funktion VBUniqRandInt VBUniqRandInt verwendet und mit 500.000 Iterationen sehr wahrscheinlich (aber nicht sicher) alle Möglichkeiten ermittelt. Eine dritte Möglichkeit bestünde in der Nutzung der Funktion Kombinationen_mit_Subsets_k_von_n, um alle möglichen 84 * 84 * 20 = 141,120 Permutationen durchzugehen.

Eine (von 12 verschiedenen) kombinierte Entnahme mit der geringsten Restgewichtssumme ist:

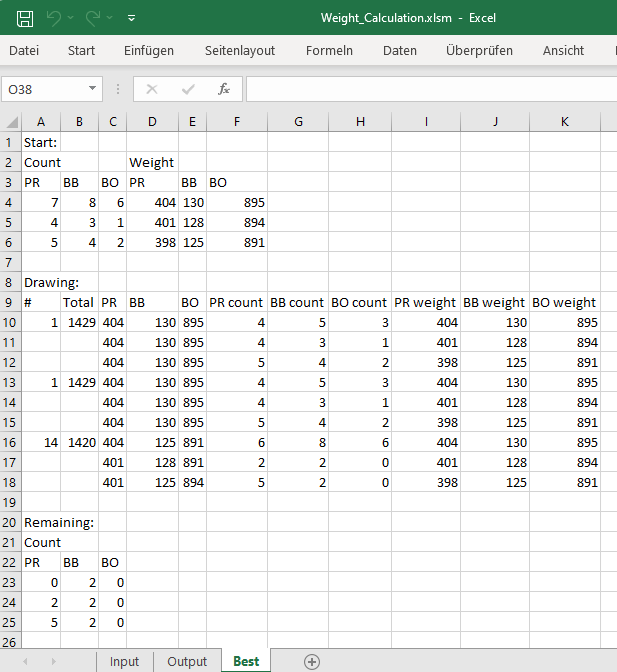
weight_calculation_best

Alle 12 verschiedenen Entnahmekombinationen - die Nummern beziehen sich auf die o. g. Ausgabevariante:

Erste Ziehung	Zweite Ziehung	Dritte Ziehung
1	1	14
1	1	16
1	1	21
1	1	24
1	2	23
1	3	19
1	5	7
1	5	13
1	5	20
1	6	19
1	9	12
2	5	19

Appendix – Programmcode AllFirstDraws und CombinationsWithMinRemainingWeight

Bitte den Haftungsausschluss im Impressum beachten.

Option Explicit

'Calculates 3 * 3 - tuples of same total weights.
'Source (EN): https://www.sulprobil.de/weight_calculation_en/
'Source (DE): https://www.berndplumhoff.de/gewichtberechnung_de/
'(C) (P) by Bernd Plumhoff 26-Jun-2024 PB V0.4

Sub AllFirstDraws()
Dim i                          As Long
Dim j                          As Long
Dim k                          As Long
Dim i2                         As Long
Dim j2                         As Long
Dim k2                         As Long
Dim i3                         As Long
Dim j3                         As Long
Dim k3                         As Long
Dim m                          As Long
Dim n                          As Long
Dim t                          As Long
Dim v                          As Long

Dim oGetRidofDupes             As Object

Dim vCount                     As Variant
Dim vWeight                    As Variant

Dim state                      As SystemState

With Application.WorksheetFunction
Set state = New SystemState
wsI.Cells.EntireColumn.AutoFit
wsO.Cells.ClearContents
Set oGetRidofDupes = CreateObject("Scripting.Dictionary")
i = 1
Do While wsI.Cells(2, i) <> ""
  i = i + 1
Loop
n = (i - 1) \ 2
vCount = .Transpose(Range(wsI.Cells(3, 1), wsI.Cells(3, n).End(xlDown)))
vWeight = .Transpose(Range(wsI.Cells(3, n + 1), wsI.Cells(3, 2 * n).End(xlDown)))
For i = 1 To n
  k = 0
  For j = 1 To UBound(vCount, 2)
    k = k + vCount(j, i)
  Next j
  If k < n Then
    Call MsgBox("Not enough items in column " & i, vbOKOnly, "Error")
    Exit Sub
  End If
Next i
m = j - 1
'Debug.Print "n = " & n, "m = " & m
'Now we know the dimensions
ReDim sItem(1 To n) As String
wsO.Cells(1, 1) = "#"
wsO.Cells(1, 2) = "Total"
For i = 1 To n
  sItem(i) = wsI.Cells(2, i)
  wsO.Cells(1, i + 2) = sItem(i)
  wsO.Cells(1, n + 2 + i) = sItem(i) & " count"
  wsO.Cells(1, 2 * n + 2 + i) = sItem(i) & " weight"
Next i

ReDim lPermutWeight(1 To n, 1 To n * m) As Long
ReDim lPermutIdx(1 To n) As Long
ReDim lPermutSubGroupIdx(1 To n, 1 To n * m) As Long

For i = 1 To n
  t = 0
  For j = 1 To m
    For k = 1 To .Min(n, vCount(i, j))
      t = t + 1
      lPermutWeight(i, t) = vWeight(i, j)
      lPermutSubGroupIdx(i, t) = j
    Next k
  Next j
  lPermutIdx(i) = t
Next i

v = 2
For i = 1 To lPermutIdx(1)
  For j = 1 To lPermutIdx(1)
    If j <> i Then
      For k = 1 To lPermutIdx(1)
        If k <> j And k <> i Then
          For i2 = 1 To lPermutIdx(2)
            For j2 = 1 To lPermutIdx(2)
              If j2 <> i2 Then
                For k2 = 1 To lPermutIdx(2)
                  If k2 <> j2 And k2 <> i2 Then
                    For i3 = 1 To lPermutIdx(3)
                      For j3 = 1 To lPermutIdx(3)
                        If j3 <> i3 Then
                          For k3 = 1 To lPermutIdx(3)
                            If k3 <> j3 And k3 <> i3 Then
                              'Debug.Print lPermutWeight(1, i) & " + " & lPermutWeight(2, i2) & " + " & lPermutWeight(3, i3) & " ?= " & lPermutWeight(1, j) & " + " & lPermutWeight(2, j2) & " + " & lPermutWeight(3, j3) & " And " & lPermutWeight(1, i) & " + " & lPermutWeight(2, i2) & " + " & lPermutWeight(3, i3) & " ?= " & lPermutWeight(1, k) & " + " & lPermutWeight(2, k2) & " + " & lPermutWeight(3, k3)
                              If lPermutWeight(1, i) + lPermutWeight(2, i2) + lPermutWeight(3, i3) = _
                                 lPermutWeight(1, j) + lPermutWeight(2, j2) + lPermutWeight(3, j3) And _
                                 lPermutWeight(1, i) + lPermutWeight(2, i2) + lPermutWeight(3, i3) = _
                                 lPermutWeight(1, k) + lPermutWeight(2, k2) + lPermutWeight(3, k3) Then
                                 If Not oGetRidofDupes.exists(lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
                                    lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
                                    lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3)) Then
                                    oGetRidofDupes(lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
                                      lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
                                      lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3)) = 1
                                    oGetRidofDupes(lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
                                      lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
                                      lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3)) = 1
                                    oGetRidofDupes(lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
                                      lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
                                      lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3)) = 1
                                    oGetRidofDupes(lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
                                      lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
                                      lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3)) = 1
                                    oGetRidofDupes(lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
                                      lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
                                      lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3)) = 1
                                    oGetRidofDupes(lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
                                      lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
                                      lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3)) = 1
                                    wsO.Cells(v, 1) = (v + 1) \ n
                                    wsO.Cells(v, 2) = lPermutWeight(1, i) + lPermutWeight(2, i2) + lPermutWeight(3, i3)
                                    wsO.Cells(v, 3) = lPermutWeight(1, i)
                                    wsO.Cells(v, 4) = lPermutWeight(2, i2)
                                    wsO.Cells(v, 5) = lPermutWeight(3, i3)
                                    wsO.Cells(v + 1, 3) = lPermutWeight(1, j)
                                    wsO.Cells(v + 1, 4) = lPermutWeight(2, j2)
                                    wsO.Cells(v + 1, 5) = lPermutWeight(3, j3)
                                    wsO.Cells(v + 2, 3) = lPermutWeight(1, k)
                                    wsO.Cells(v + 2, 4) = lPermutWeight(2, k2)
                                    wsO.Cells(v + 2, 5) = lPermutWeight(3, k3)
                                    wsO.Cells(v, 6) = vCount(1, 1) - IIf(lPermutSubGroupIdx(1, i) = 1, 1, 0) - IIf(lPermutSubGroupIdx(1, j) = 1, 1, 0) - IIf(lPermutSubGroupIdx(1, k) = 1, 1, 0)
                                    wsO.Cells(v, 7) = vCount(2, 1) - IIf(lPermutSubGroupIdx(2, i2) = 1, 1, 0) - IIf(lPermutSubGroupIdx(2, j2) = 1, 1, 0) - IIf(lPermutSubGroupIdx(2, k2) = 1, 1, 0)
                                    wsO.Cells(v, 8) = vCount(3, 1) - IIf(lPermutSubGroupIdx(3, i3) = 1, 1, 0) - IIf(lPermutSubGroupIdx(3, j3) = 1, 1, 0) - IIf(lPermutSubGroupIdx(3, k3) = 1, 1, 0)
                                    wsO.Cells(v + 1, 6) = vCount(1, 2) - IIf(lPermutSubGroupIdx(1, i) = 2, 1, 0) - IIf(lPermutSubGroupIdx(1, j) = 2, 1, 0) - IIf(lPermutSubGroupIdx(1, k) = 2, 1, 0)
                                    wsO.Cells(v + 1, 7) = vCount(2, 2) - IIf(lPermutSubGroupIdx(2, i2) = 2, 1, 0) - IIf(lPermutSubGroupIdx(2, j2) = 2, 1, 0) - IIf(lPermutSubGroupIdx(2, k2) = 2, 1, 0)
                                    wsO.Cells(v + 1, 8) = vCount(3, 2) - IIf(lPermutSubGroupIdx(3, i3) = 2, 1, 0) - IIf(lPermutSubGroupIdx(3, j3) = 2, 1, 0) - IIf(lPermutSubGroupIdx(3, k3) = 2, 1, 0)
                                    wsO.Cells(v + 2, 6) = vCount(1, 3) - IIf(lPermutSubGroupIdx(1, i) = 3, 1, 0) - IIf(lPermutSubGroupIdx(1, j) = 3, 1, 0) - IIf(lPermutSubGroupIdx(1, k) = 3, 1, 0)
                                    wsO.Cells(v + 2, 7) = vCount(2, 3) - IIf(lPermutSubGroupIdx(2, i2) = 3, 1, 0) - IIf(lPermutSubGroupIdx(2, j2) = 3, 1, 0) - IIf(lPermutSubGroupIdx(2, k2) = 3, 1, 0)
                                    wsO.Cells(v + 2, 8) = vCount(3, 3) - IIf(lPermutSubGroupIdx(3, i3) = 3, 1, 0) - IIf(lPermutSubGroupIdx(3, j3) = 3, 1, 0) - IIf(lPermutSubGroupIdx(3, k3) = 3, 1, 0)
                                    wsO.Cells(v, 9) = vWeight(1, 1)
                                    wsO.Cells(v, 10) = vWeight(2, 1)
                                    wsO.Cells(v, 11) = vWeight(3, 1)
                                    wsO.Cells(v + 1, 9) = vWeight(1, 2)
                                    wsO.Cells(v + 1, 10) = vWeight(2, 2)
                                    wsO.Cells(v + 1, 11) = vWeight(3, 2)
                                    wsO.Cells(v + 2, 9) = vWeight(1, 3)
                                    wsO.Cells(v + 2, 10) = vWeight(2, 3)
                                    wsO.Cells(v + 2, 11) = vWeight(3, 3)
                                    v = v + 3
                                 End If
                              End If
                            End If
                          Next k3
                        End If
                      Next j3
                    Next i3
                  End If
                Next k2
              End If
            Next j2
          Next i2
        End If
      Next k
    End If
  Next j
Next i
wsO.Cells.EntireColumn.AutoFit
End With
End Sub

Sub CombinationsWithMinRemainingWeight()

Dim i                          As Long
Dim j                          As Long
Dim k                          As Long
Dim m                          As Long
Dim maxsum                     As Long
Dim n                          As Long
Dim sum(1 To 33)               As Long
Dim t                          As Long
Dim u                          As Long
Dim v                          As Long
Dim w                          As Long

Dim vCount                     As Variant
Dim vC(1 To 33)                As Variant
Dim vCi(1 To 3)                As Variant

Dim state                      As SystemState

With Application.WorksheetFunction
Set state = New SystemState

i = 1
Do While wsI.Cells(2, i) <> ""
  i = i + 1
Loop
n = (i - 1) \ 2
vCount = .Transpose(.Transpose(Range(wsI.Cells(3, 1), wsI.Cells(3, n).End(xlDown))))
For i = 1 To n
  k = 0
  For j = 1 To UBound(vCount, 2)
    k = k + vCount(j, i)
  Next j
  If k < n Then
    Call MsgBox("Not enough items in column " & i, vbOKOnly, "Error")
    Exit Sub
  End If
Next i
m = j - 1

i = 2
t = wsO.Cells(i, 1)
Do While t <> 0
  sum(t) = wsO.Cells(i, 2)
  vC(t) = .Transpose(.Transpose(Range(wsO.Cells(i, 6), wsO.Cells(i + 2, 8))))
  i = i + 3
  t = wsO.Cells(i, 1)
Loop

t = 0
maxsum = 0
For i = 1 To 33
  vCi(1) = vC(i)
  For j = 1 To 33
    vCi(2) = vCi(1)
    For m = 1 To 3
      For n = 1 To 3
        If vCi(1)(m, n) < vCount(m, n) - vC(j)(m, n) Then GoTo Label_Next_j
        vCi(2)(m, n) = vCi(1)(m, n) - vCount(m, n) + vC(j)(m, n)
      Next n
    Next m
    For k = 1 To 33
      vCi(3) = vCi(2)
      For m = 1 To 3
        For n = 1 To 3
          If vCi(2)(m, n) < vCount(m, n) - vC(k)(m, n) Then GoTo Label_Next_k
          vCi(3)(m, n) = vCi(2)(m, n) - vCount(m, n) + vC(k)(m, n)
        Next n
      Next m
      
      If maxsum <= 3 * (sum(i) + sum(j) + sum(k)) Then
        maxsum = 3 * (sum(i) + sum(j) + sum(k))
        t = t + 1
        Debug.Print t, maxsum, i, j, k
      End If
      
Label_Next_k:
    Next k
Label_Next_j:
  Next j
Next i

End With

End Sub