Abstract
Dieser Algorithmus erzeugt alle Kombinationen von k Elementen aus einer Gesamtmenge mit n Elementen.
Während die Excel Funktion KOMBINATIONEN(n; k) die Anzahl dieser Kombinationen anzeigt, listet der hier vorgestellte Algorithmus alle einzeln, damit sie ggf. untersucht werden können. Das vorgestellte Programm ist schnell - zum Vergleich siehe unten die unter Weitere Links zu findenden Formelansätze.
Beispiel
Eingabe:
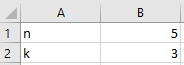
Ausgabe:
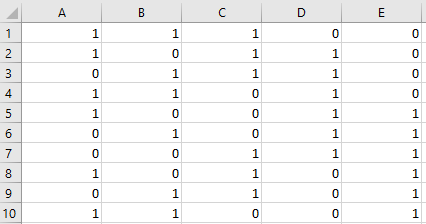
Literatur
Reingold, Nievergelt, Deo: Combinatorial Algorithms, 1977, Algorithm 5.9, p. 186, ISBN 0-13-152447-X
Weitere Links
(Externer Link!) Efficient approach to generate list of combinations with no repetition
Appendix – Programmcode Combinations_with_k_subsets_of_n
Bitte den Haftungsausschluss im Impressum beachten.
Option Explicit
Public r As Long 'Output row
'Generates all combinations of array n with subsets k.
'See Reingold, Nievergelt, Deo: Combinatorial Algorithms, 1977, Algorithm 5.9, p. 186, ISBN 0-13-152447-X
'Version 0.2 12-Jul-2024
Sub Combinations_with_k_subsets_of_n(n As Long, k As Long)
Dim i As Long, j As Long, m As Long, t As Long, u As Long
With Application.WorksheetFunction
wsO.Cells.ClearContents
ReDim g(1 To n + 1) As Long
ReDim tau(1 To n + 1) As Long
ReDim res(1 To .Combin(n, k), 1 To n) As Variant
r = 1
For j = 1 To k
g(j) = 1
tau(j) = j + 1
Next j
For j = k + 1 To n + 1
g(j) = 0
tau(j) = j + 1
Next j
t = k
tau(1) = k + 1
i = 0
Do While i <> n + 1
'Call Visit(g) instead of the next 4 rows if you need to analyze g().
For u = 1 To UBound(g) - 1
res(r, u) = g(u)
Next u
r = r + 1
i = tau(1)
tau(1) = tau(i)
tau(i) = i + 1
If g(i) = 1 Then
If t <> 0 Then
g(t) = 1 - g(t)
Else
g(i - 1) = 1 - g(i - 1)
End If
t = t + 1
Else
If t <> 1 Then
g(t - 1) = 1 - g(t - 1)
Else
g(i - 1) = 1 - g(i - 1)
End If
t = t - 1
End If
g(i) = 1 - g(i)
If t = i - 1 Or t = 0 Then
t = t + 1
Else
t = t - g(i - 1)
tau(i - 1) = tau(1)
If t = 0 Then
tau(1) = i - 1
Else
tau(1) = t + 1
End If
End If
Loop
Range(wsO.Cells(1, 1), wsO.Cells(r - 1, n)) = res
End With
End Sub
Sub Visit(g As Variant)
'Print current permutation in immediate window and on sheet Output.
'You can analyze the permutation or do other things as well.
Dim i As Long
For i = 1 To UBound(g) - 1
wsO.Cells(r, i) = g(i)
Debug.Print g(i);
Next i
Debug.Print
r = r + 1
End Sub
Sub test()
Debug.Print Now
Call Combinations_with_k_subsets_of_n(5, 3)
Debug.Print Now
End Sub
Download
Bitte den Haftungsausschluss im Impressum beachten.
combinations_with_k_subsets_of_n.xlsm [26 KB Excel Datei, ohne jegliche Gewährleistung]