Optionen (VBA) ·

Abstract

Ein klassisches Buch zur Bewertung von Optionen ist

Les Clewlow and Chris Strickland: Implementing Derivatives Models (ISBN 0471966517)

Leider enthält dieses Buch eine Vielzahl von Fehlern, und die 8 Seiten lange Fehlerliste vom 23. November 2000 scheint auch nicht mehr öffentlich verfügbar zu sein.

Einige Fehlerkorrekturen für die erste Auflage:

Page	Row	Correction
xvi	9, column 3	0v should be C
12	15	Si,j = Su^jd^(n-j)
24	2 from top in figure 2.12	set coefficients
70	4 from bottom in figure 3.13	for j =Nj-2 downto -Nj+1 do
70	Insert before last row of figure 3.13	C[1,-Nj] = C[1,-Nj + 1] - lambda_L
75	4 from bottom in figure 3.16	for j =Nj-2 downto -Nj+1 do
75	Insert before last row of figure 3.16	C[1,-Nj] = C[1,-Nj + 1] - lambda_L
85	2 from bottom in figure 4.2	SD = sqrt( (-sum_CT2 + sum_CT * sum_CT / M ) ) * exp(-2rT) / (M - 1)
89	2 from bottom in figure 4.5	SD = sqrt( (-sum_CT2 + sum_CT * sum_CT / M ) ) * exp(-2rT) / (M - 1)
99	Delete row 9 from top	lnS = ln(S) = 4.6052 <- delete this row
113	13 from top in figure 4.19	Insert before for j loop V1 = sig1sig1; V2 = sig2sig2
113	18 from top in figure 4.19	Insert before for i loop Vt1 = V1; Vt2 = V2
118	Last row	a = m/N * ln(Gt) …
120	11 from bottom in figure 4.24	G = productSt ^(1/N)

Ich implementierte einige der im Buch vorgestellten Algorithmen mit Excel VBA.

Das Binomialbaummodell

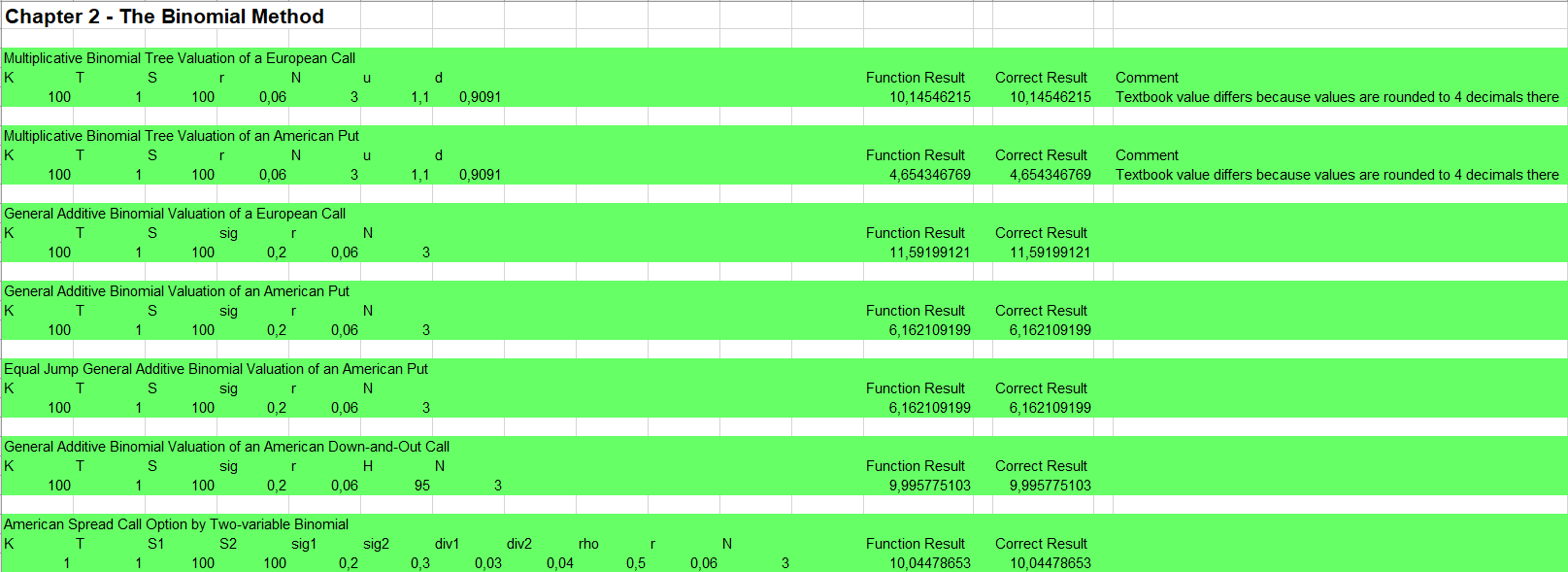
Clewlow_Strickland_Chapter2

Bitte den Haftungsausschluss im Impressum beachten.

Function European_Call_MBTV( _
    K As Double, _
    T As Double, _
    S As Double, _
    r As Double, _
    N As Long, _
    u As Double, _
    d As Double) As Double

'Multiplicative Binomial Tree Valuation of a European Call
'Clewlow/Strickland: Implementing Derivatives Models, page 13
'ISBN 0-471-96651-7
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim p As Double
Dim disc As Double
ReDim St(0 To N) As Double
ReDim C(0 To N) As Double
Dim i As Long, j As Long

'precompute constants

dt = T / N
p = (Exp(r * dt) - d) / (u - d)
disc = Exp(-r * dt)

'Debug.Print dt, p, disc

'initialise asset prices at maturity time step N

St(0) = S * d ^ N
For j = 1 To N
    St(j) = St(j - 1) * u / d
Next j

'Debug.Print St(0), St(1), St(2), St(3)

'initialise option values at maturity

For j = 0 To N
    C(j) = St(j) - K: If C(j) < 0# Then C(j) = 0#
Next j

'Debug.Print C(0), C(1), C(2), C(3)

'step back through the tree

For i = N - 1 To 0 Step -1
    For j = 0 To i
        C(j) = disc * (p * C(j + 1) + (1 - p) * C(j))
        'Debug.Print C(j);
    Next j
    'Debug.Print
Next i

European_Call_MBTV = C(0)

End Function

Function American_Put_MBTV( _
    K As Double, _
    T As Double, _
    S As Double, _
    r As Double, _
    N As Long, _
    u As Double, _
    d As Double) As Double

'Multiplicative Binomial Tree Valuation of an American Put
'Clewlow/Strickland: Implementing Derivatives Models, page 15
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim p As Double
Dim disc As Double
ReDim St(0 To N) As Double
ReDim C(0 To N) As Double
Dim i As Long, j As Long

'precompute constants

dt = T / N
p = (Exp(r * dt) - d) / (u - d)
disc = Exp(-r * dt)

'Debug.Print dt, p, disc

'initialise asset prices at maturity time step N

St(0) = S * d ^ N
For j = 1 To N
    St(j) = St(j - 1) * u / d
Next j

'Debug.Print St(0), St(1), St(2), St(3)

'initialise option values at maturity

For j = 0 To N
    C(j) = K - St(j): If C(j) < 0# Then C(j) = 0#
Next j

'Debug.Print C(0), C(1), C(2), C(3)

'step back through the tree applying the early exercise condition

For i = N - 1 To 0 Step -1
    For j = 0 To i
        C(j) = disc * (p * C(j + 1) + (1 - p) * C(j))
        St(j) = St(j) / d
        If C(j) < K - St(j) Then C(j) = K - St(j)
        'Debug.Print C(j);
    Next j
    'Debug.Print
Next i

American_Put_MBTV = C(0)

End Function

Function European_Call_GABV( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    N As Long) As Double

'General Additive Binomial Valuation of a European Call
'Clewlow/Strickland: Implementing Derivatives Models, page 22
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pd As Double
Dim dxu As Double, dxd As Double, nu As Double
Dim disc As Double
ReDim St(0 To N) As Double
ReDim C(0 To N) As Double
Dim i As Long, j As Long

'set coefficients - Trigeorgis

dt = T / N
nu = r - 0.5 * sig ^ 2#
dxu = Sqr(sig ^ 2# * dt + (nu * dt) ^ 2#)
dxd = -dxu
pu = 0.5 + 0.5 * (nu * dt / dxu)
pd = 1# - pu

'precompute constants

disc = Exp(-r * dt)

'initialise asset prices at maturity N

St(0) = S * Exp(N * dxd)
For j = 1 To N
    St(j) = St(j - 1) * Exp(dxu - dxd)
Next j
'Debug.Print St(0), St(1), St(2), St(3)

'initialise option values at maturity

For j = 0 To N
    C(j) = St(j) - K: If C(j) < 0# Then C(j) = 0#
Next j
'Debug.Print C(0), C(1), C(2), C(3)

'step back through the tree

For i = N - 1 To 0 Step -1
    For j = 0 To i
        C(j) = disc * (pu * C(j + 1) + pd * C(j))
        'Debug.Print C(j);
    Next j
    'Debug.Print
Next i

European_Call_GABV = C(0)

End Function

Function American_Put_GABV( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    N As Long) As Double

'General Additive Binomial Valuation of an American Put
'Clewlow/Strickland: Implementing Derivatives Models, page 24
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pd As Double
Dim dxu As Double, dxd As Double, nu As Double
Dim disc As Double
ReDim St(0 To N) As Double
ReDim C(0 To N) As Double
Dim i As Long, j As Long

'set coefficients - Trigeorgis

dt = T / N
nu = r - 0.5 * sig ^ 2#
dxu = Sqr(sig ^ 2 * dt + (nu * dt) ^ 2#)
dxd = -dxu
pu = 0.5 + 0.5 * (nu * dt / dxu)
pd = 1# - pu

'precompute constants

disc = Exp(-r * dt)

'initialise asset prices at maturity N

St(0) = S * Exp(N * dxd)
For j = 1 To N
    St(j) = St(j - 1) * Exp(dxu - dxd)
Next j
'Debug.Print St(0), St(1), St(2), St(3)

'initialise option values at maturity

For j = 0 To N
    C(j) = K - St(j): If C(j) < 0# Then C(j) = 0#
Next j
'Debug.Print C(0), C(1), C(2), C(3)

'step back through the tree applying the early exercise condition

For i = N - 1 To 0 Step -1
    For j = 0 To i
        C(j) = disc * (pu * C(j + 1) + pd * C(j))
        'adjust asset price to current time step
        St(j) = St(j) / Exp(dxd)
        'apply the early exercise condition
        If K - St(j) > C(j) Then C(j) = K - St(j)
        'Debug.Print C(j);
    Next j
    'Debug.Print
Next i

American_Put_GABV = C(0)

End Function

Function American_Put_EJGABV( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    N As Long) As Double

'Equal Jump General Additive Binomial Valuation of an American Put
'Clewlow/Strickland: Implementing Derivatives Models, page 28
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pd As Double
Dim dx As Double, nu As Double
Dim disc As Double, edx As Double
Dim dpu As Double, dpd As Double
ReDim St(-N To N) As Double
ReDim C(-N To N) As Double
Dim i As Long, j As Long

'set coefficients - Trigeorgis

dt = T / N
nu = r - 0.5 * sig ^ 2#
dx = Sqr(sig ^ 2# * dt + (nu * dt) ^ 2#)
pu = 0.5 + 0.5 * (nu * dt / dx)
pd = 1# - pu

'precompute constants

disc = Exp(-r * dt)
dpu = disc * pu
dpd = disc * pd
edx = Exp(dx)

'initialise asset prices at maturity N

St(-N) = S * Exp(-N * dx)
For j = -N + 1 To N
    St(j) = St(j - 1) * edx
Next j

'initialise option values at maturity

For j = -N To N Step 2
    C(j) = K - St(j): If C(j) < 0# Then C(j) = 0#
Next j

'step back through the tree applying the early exercise condition

For i = N - 1 To 0 Step -1
    For j = -i To i Step 2
        C(j) = dpd * C(j - 1) + dpu * C(j + 1)
        'apply the early exercise condition
        If K - St(j) > C(j) Then C(j) = K - St(j)
    Next j
Next i

American_Put_EJGABV = C(0)

End Function

Function American_Down_and_Out_Call_GABV( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    H As Double, _
    N As Long) As Double

'General Additive Binomial Valuation of an American Down-and-Out Call
'Clewlow/Strickland: Implementing Derivatives Models, page 41
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pd As Double
Dim dpu As Double, dpd As Double
Dim dxd As Double, dxu As Double, nu As Double
Dim edxud As Double
Dim edxd As Double
Dim disc As Double
ReDim St(0 To N) As Double
ReDim C(0 To N) As Double
Dim i As Long, j As Long

'set coefficients - Trigeorgis

dt = T / N
nu = r - 0.5 * sig ^ 2#
dxu = Sqr(sig ^ 2# * dt + (nu * dt) ^ 2#)
dxd = -dxu
pu = 0.5 + 0.5 * (nu * dt / dxu)
pd = 1# - pu

'precompute constants

disc = Exp(-r * dt)
dpu = disc * pu
dpd = disc * pd
edxud = Exp(dxu - dxd)
edxd = Exp(dxd)

'initialise asset prices at maturity N

St(0) = S * Exp(N * dxd)
For j = 1 To N
    St(j) = St(j - 1) * edxud
Next j

'initialise option values at maturity

For j = 0 To N
    If St(j) > H Then
        C(j) = St(j) - K: If C(j) < 0# Then C(j) = 0#
    Else
        C(j) = 0#
    End If
Next j

'step back through the tree applying the barrier
'and early exercise condition

For i = N - 1 To 0 Step -1
    For j = 0 To i
        'adjust asset price to current time step
        St(j) = St(j) / edxd
        
        If St(j) > H Then
            C(j) = dpd * C(j) + dpu * C(j + 1)
            
            'apply the early exercise condition
            If C(j) < St(j) - K Then C(j) = St(j) - K
        Else
            C(j) = 0#
        End If
    Next j
Next i

American_Down_and_Out_Call_GABV = C(0)

End Function

Function American_Spread_Call_Option_bTvB( _
    K As Double, _
    T As Double, _
    S1 As Double, _
    S2 As Double, _
    sig1 As Double, _
    sig2 As Double, _
    div1 As Double, _
    div2 As Double, _
    rho As Double, _
    r As Double, _
    N As Long) As Double

'American Spread Call Option by Two-variable Binomial
'Clewlow/Strickland: Implementing Derivatives Models, page 46
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim puu As Double, pdu As Double
Dim pud As Double, pdd As Double
Dim dx1 As Double, dx2 As Double
Dim nu1 As Double, nu2 As Double
Dim edx1 As Double, edx2 As Double
Dim disc As Double
ReDim s1t(-N To N) As Double
ReDim s2t(-N To N) As Double
ReDim C(-N To N, -N To N) As Double
Dim i As Long, j As Long, k1 As Long

'precompute constants

dt = T / N
nu1 = r - div1 - 0.5 * sig1 ^ 2#
nu2 = r - div2 - 0.5 * sig2 ^ 2#
dx1 = sig1 * Sqr(dt)
dx2 = sig2 * Sqr(dt)
disc = Exp(-r * dt)
puu = (dx1 * dx2 + (dx2 * nu1 + dx1 * nu2 + rho * sig1 * sig2) * dt) / _
        (4 * dx1 * dx2) * disc
pud = (dx1 * dx2 + (dx2 * nu1 - dx1 * nu2 - rho * sig1 * sig2) * dt) / _
        (4 * dx1 * dx2) * disc
pdu = (dx1 * dx2 - (dx2 * nu1 - dx1 * nu2 + rho * sig1 * sig2) * dt) / _
        (4 * dx1 * dx2) * disc
pdd = (dx1 * dx2 - (dx2 * nu1 + dx1 * nu2 - rho * sig1 * sig2) * dt) / _
        (4 * dx1 * dx2) * disc
edx1 = Exp(dx1)
edx2 = Exp(dx2)

'initialise asset prices at time step N

s1t(-N) = S1 * Exp(-N * dx1)
s2t(-N) = S2 * Exp(-N * dx2)
For j = -N + 1 To N
    s1t(j) = s1t(j - 1) * edx1
    s2t(j) = s2t(j - 1) * edx2
Next j

'initialise option values at maturity

For j = -N To N Step 2
    For k1 = -N To N Step 2
        C(j, k1) = s1t(j) - s2t(k1) - K
        If C(j, k1) < 0# Then C(j, k1) = 0#
    Next k1
Next j

'step back through the tree applying the early exercise condition

For i = N - 1 To 0 Step -1
    For j = -i To i Step 2
        For k1 = -i To i Step 2
            C(j, k1) = pdd * C(j - 1, k1 - 1) + pud * C(j + 1, k1 - 1) + _
                        pdu * C(j - 1, k1 + 1) + puu * C(j + 1, k1 + 1)
            'apply the early exercise condition
            If s1t(j) - s2t(k1) - K > C(j, k1) Then C(j, k1) = s1t(j) - s2t(k1) - K
        Next k1
    Next j
Next i

American_Spread_Call_Option_bTvB = C(0, 0)

End Function

Das Trinomial-Optionspreismodell und die Methode der Finiten Differenzen

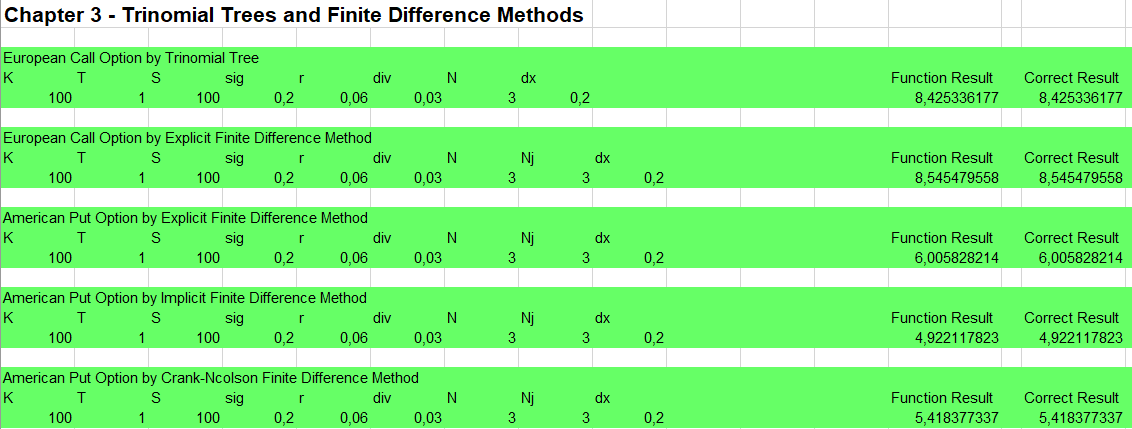
Clewlow_Strickland_Chapter3

Bitte den Haftungsausschluss im Impressum beachten.

Function European_Call_Option_bTT( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    dx As Double) As Double

'European Call Option by Trinomial Tree
'Clewlow/Strickland: Implementing Derivatives Models, page 54
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pm As Double, pd As Double
Dim nu As Double, edx As Double
Dim disc As Double
ReDim St(-N To N) As Double
ReDim C(0 To N, -N To N) As Double
Dim i As Long, j As Long

'set coefficients - Trigeorgis

dt = T / N
nu = r - div - 0.5 * sig ^ 2#
edx = Exp(dx)
pu = 0.5 * ((sig ^ 2# * dt + nu ^ 2# * dt ^ 2#) / dx ^ 2# + nu * dt / dx)
pm = 1# - (sig ^ 2# * dt + nu ^ 2# * dt ^ 2#) / dx ^ 2#
pd = 0.5 * ((sig ^ 2# * dt + nu ^ 2# * dt ^ 2#) / dx ^ 2# - nu * dt / dx)
disc = Exp(-r * dt)

'initialise asset prices at maturity N

St(-N) = S * Exp(-N * dx)
For j = -N + 1 To N
    St(j) = St(j - 1) * edx
Next j

'initialise option values at maturity

For j = -N To N
    If St(j) - K > 0# Then
        C(N, j) = St(j) - K
    Else
        C(N, j) = 0#
    End If
Next j

'step back through lattice

For i = N - 1 To 0 Step -1
    For j = -i To i
        C(i, j) = disc * (pu * C(i + 1, j + 1) + pm * C(i + 1, j) + pd * C(i + 1, j - 1))
    Next j
Next i

European_Call_Option_bTT = C(0, 0)

End Function

Function European_Call_Option_bEFDM( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    Nj As Long, _
    dx As Double) As Double

'European Call Option by Explicit Finite Difference Method
'Clewlow/Strickland: Implementing Derivatives Models, page 60
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pm As Double, pd As Double
Dim nu As Double, edx As Double
ReDim St(-Nj To Nj) As Double
ReDim C(0 To N, -Nj To Nj) As Double
Dim i As Long, j As Long

'set coefficients - Trigeorgis

dt = T / N
nu = r - div - 0.5 * sig ^ 2#
edx = Exp(dx)
pu = 0.5 * dt * ((sig / dx) ^ 2# + nu / dx)
pm = 1# - dt * ((sig / dx) ^ 2# + r)
pd = 0.5 * dt * ((sig / dx) ^ 2# - nu / dx)

'initialise asset prices at maturity N

St(-Nj) = S * Exp(-Nj * dx)
For j = -Nj + 1 To Nj
    St(j) = St(j - 1) * edx
Next j

'initialise option values at maturity

For j = -Nj To Nj
    If St(j) - K > 0# Then
        C(N, j) = St(j) - K
    Else
        C(N, j) = 0#
    End If
Next j

'step back through lattice

For i = N - 1 To 0 Step -1
    For j = -Nj + 1 To Nj - 1
        C(i, j) = pu * C(i + 1, j + 1) + pm * C(i + 1, j) + pd * C(i + 1, j - 1)
    Next j
    'boundary conditions
    C(i, -Nj) = C(i, -Nj + 1)
    C(i, Nj) = C(i, Nj - 1) + St(Nj) - St(Nj - 1)
Next i

European_Call_Option_bEFDM = C(0, 0)

End Function

Function American_Put_Option_bEFDM( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    Nj As Long, _
    dx As Double) As Double

'American Put Option by Explicit Finite Difference Method
'Clewlow/Strickland: Implementing Derivatives Models, page 62
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pm As Double, pd As Double
Dim nu As Double, edx As Double
ReDim St(-Nj To Nj) As Double
ReDim C(0 To 1, -Nj To Nj) As Double
Dim i As Long, j As Long

'Precompute constants

dt = T / N
nu = r - div - 0.5 * sig ^ 2#
edx = Exp(dx)
pu = 0.5 * dt * ((sig / dx) ^ 2# + nu / dx)
pm = 1# - dt * (sig / dx) ^ 2# - r * dt
pd = 0.5 * dt * ((sig / dx) ^ 2# - nu / dx)

'Initialise asset prices at maturity N

St(-Nj) = S * Exp(-Nj * dx)
For j = -Nj + 1 To Nj
    St(j) = St(j - 1) * edx
Next j

'Initialise option values at maturity

For j = -Nj To Nj
    If K - St(j) > 0# Then
        C(0, j) = K - St(j)
    Else
        C(0, j) = 0#
    End If
Next j

'Step back through lattice

For i = N - 1 To 0 Step -1

    For j = -Nj + 1 To Nj - 1
        C(1, j) = pu * C(0, j + 1) + pm * C(0, j) + pd * C(0, j - 1)
    Next j
    
    'Boundary conditions
    
    C(1, -Nj) = C(1, -Nj + 1) + St(-Nj + 1) - St(-Nj)
    C(1, Nj) = C(1, Nj - 1)
    
    'Apply early exercise condition
    
    For j = -Nj To Nj
        C(0, j) = K - St(j)
        If C(0, j) < C(1, j) Then C(0, j) = C(1, j)
    Next j
    
Next i

American_Put_Option_bEFDM = C(0, 0)

End Function

Function American_Put_Option_bIFDM( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    Nj As Long, _
    dx As Double) As Double

'American Put Option by Implicit Finite Difference Method
'Clewlow/Strickland: Implementing Derivatives Models, page 69
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pm As Double, pd As Double
Dim nu As Double, edx As Double
Dim lambda_L As Double, lambda_U As Double
ReDim St(-Nj To Nj) As Double
ReDim C(0 To 1, -Nj To Nj) As Double
Dim i As Long, j As Long
ReDim pmp(-Nj To Nj) As Double
ReDim pp(-Nj To Nj) As Double

'Precompute constants

dt = T / N
nu = r - div - 0.5 * sig ^ 2#
edx = Exp(dx)
pu = -0.5 * dt * ((sig / dx) ^ 2# + nu / dx)
pm = 1# + dt * (sig / dx) ^ 2# + r * dt
pd = -0.5 * dt * ((sig / dx) ^ 2# - nu / dx)

'Initialise asset prices at maturity N

St(-Nj) = S * Exp(-Nj * dx)
For j = -Nj + 1 To Nj
    St(j) = St(j - 1) * edx
Next j

'Initialise option values at maturity

For j = -Nj To Nj
    If K - St(j) > 0# Then
        C(0, j) = K - St(j)
    Else
        C(0, j) = 0#
    End If
Next j

'Compute derivative boundary condition

lambda_L = St(-Nj) - St(-Nj + 1)
lambda_U = 0#

'Step back through lattice

For i = N - 1 To 0 Step -1

    'Solve implicit tridiagonal system
    
    'Substitute boundary condition at j = -Nj into j = -Nj + 1
    
    pmp(-Nj + 1) = pm + pd
    pp(-Nj + 1) = C(0, -Nj + 1) + pd * lambda_L
    
    'Eliminate upper diagonal
    
    For j = -Nj + 2 To Nj - 1
    
        pmp(j) = pm - pu * pd / pmp(j - 1)
        pp(j) = C(0, j) - pp(j - 1) * pd / pmp(j - 1)
        
    Next j
    
    'Use boundary condition at j = Nj and equation at j = Nj - 1
    
    C(1, Nj) = (pp(Nj - 1) + pmp(Nj - 1) * lambda_U) / (pu + pmp(Nj - 1))
    C(1, Nj - 1) = C(1, Nj) - lambda_U
    
    'Back-substitution
    
    For j = Nj - 2 To -Nj + 1 Step -1
        C(1, j) = (pp(j) - pu * C(1, j + 1)) / pmp(j)
    Next j
    C(1, -Nj) = C(1, -Nj + 1) - lambda_L
    
    'Apply early exercise condition
    
    For j = -Nj To Nj
        C(0, j) = K - St(j)
        If C(0, j) < C(1, j) Then C(0, j) = C(1, j)
    Next j
    
Next i

American_Put_Option_bIFDM = C(0, 0)

End Function

Function American_Put_Option_bCNFDM( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    Nj As Long, _
    dx As Double) As Double

'American Put Option by Crank-Nicolson Finite Difference Method
'Clewlow/Strickland: Implementing Derivatives Models, page 74
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim pu As Double, pm As Double, pd As Double
Dim nu As Double, edx As Double
Dim lambda_L As Double, lambda_U As Double
ReDim St(-Nj To Nj) As Double
ReDim C(0 To 1, -Nj To Nj) As Double
Dim i As Long, j As Long
ReDim pmp(-Nj To Nj) As Double
ReDim pp(-Nj To Nj) As Double

'Precompute constants

dt = T / N
nu = r - div - 0.5 * sig ^ 2#
edx = Exp(dx)
pu = -0.25 * dt * ((sig / dx) ^ 2# + nu / dx)
pm = 1# + 0.5 * dt * (sig / dx) ^ 2# + 0.5 * r * dt
pd = -0.25 * dt * ((sig / dx) ^ 2# - nu / dx)

'Initialise asset prices at maturity N

St(-Nj) = S * Exp(-Nj * dx)
For j = -Nj + 1 To Nj
    St(j) = St(j - 1) * edx
Next j

'Initialise option values at maturity

For j = -Nj To Nj
    If K - St(j) > 0# Then
        C(0, j) = K - St(j)
    Else
        C(0, j) = 0#
    End If
Next j

'Compute derivative boundary condition

lambda_L = St(-Nj) - St(-Nj + 1)
lambda_U = 0#

'Step back through lattice

For i = N - 1 To 0 Step -1

    'Solve Crank-Nicolson tridiagonal system
    
    'Substitute boundary condition at j = -Nj into j = -Nj + 1
    
    pmp(-Nj + 1) = pm + pd
    pp(-Nj + 1) = -pu * C(0, -Nj + 2) - (pm - 2) * C(0, -Nj + 1) - pd * C(0, -Nj) + pd * lambda_L
    
    'Eliminate upper diagonal
    
    For j = -Nj + 2 To Nj - 1
    
        pmp(j) = pm - pu * pd / pmp(j - 1)
        pp(j) = -pu * C(0, j + 1) - (pm - 2) * C(0, j) - pd * C(0, j - 1) - pp(j - 1) * pd / pmp(j - 1)
        
    Next j
    
    'Use boundary condition at j = Nj and equation at j = Nj - 1
    
    C(1, Nj) = (pp(Nj - 1) + pmp(Nj - 1) * lambda_U) / (pu + pmp(Nj - 1))
    C(1, Nj - 1) = C(1, Nj) - lambda_U
    
    'Back-substitution
    
    For j = Nj - 2 To -Nj + 1 Step -1
        C(1, j) = (pp(j) - pu * C(1, j + 1)) / pmp(j)
    Next j
    C(1, -Nj) = C(1, -Nj + 1) - lambda_L
    
    'Apply early exercise condition
    
    For j = -Nj To Nj
        C(0, j) = K - St(j)
        If C(0, j) < C(1, j) Then C(0, j) = C(1, j)
    Next j
    
Next i

American_Put_Option_bCNFDM = C(0, 0)

End Function

Monte Carlo Simulation

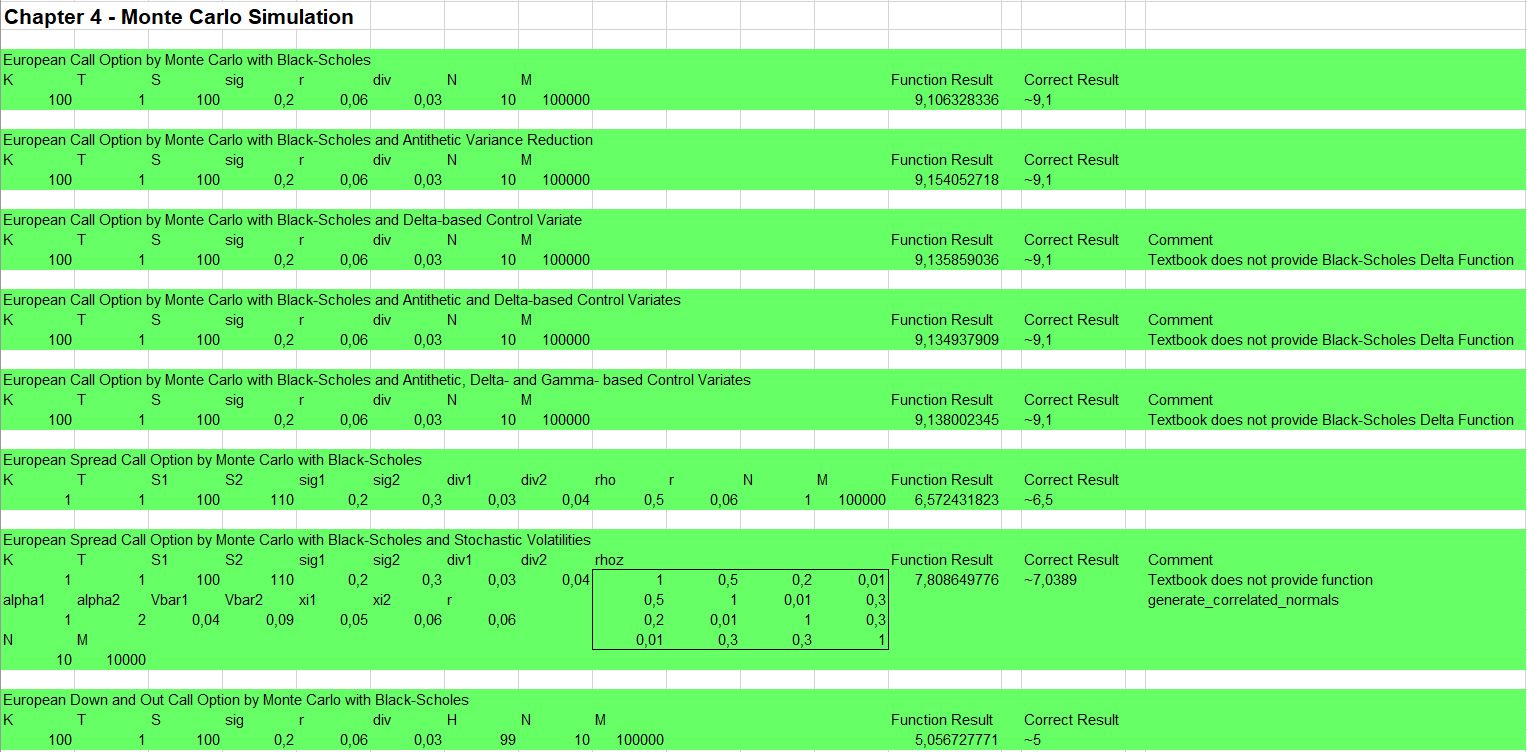
Clewlow_Strickland_Chapter4

Bitte den Haftungsausschluss im Impressum beachten.

Function European_Call_bMCBS( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    M As Long) As Double

'European Call Option by Monte Carlo with Black-Scholes
'Clewlow/Strickland: Implementing Derivatives Models, page 85
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.1

Dim dt As Double
Dim nudt As Double, sigsdt As Double
Dim lnS As Double, lnSt As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim e As Double
Dim St As Double, CT As Double
Dim SD As Double, SE As Double
Dim i As Long, j As Long

'Precompute constants

dt = T / N
nudt = (r - div - 0.5 * sig ^ 2#) * dt
sigsdt = sig * Sqr(dt)
lnS = Log(S)

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    lnSt = lnS
    
    For i = 1 To N
    
        'For each time step
        
'        e = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
        e = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
        lnSt = lnSt + nudt + sigsdt * e 'Evolve the stock price
        
    Next i
    
    St = Exp(lnSt)
    CT = St - K: If CT < 0# Then CT = 0#
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT2 + CT * CT
    
Next j

SD = Sqr(sum_CT2 - sum_CT * sum_CT / M) * Exp(-2# * r * T) / (M - 1)  'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Call_bMCBS = sum_CT / M * Exp(-r * T)

End Function

Function European_Call_bMCBS_AVR( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    M As Long) As Double

'European Call Option by Monte Carlo with Black-Scholes and Antithetic Variance Reduction
'Clewlow/Strickland: Implementing Derivatives Models, page 89
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim nudt As Double, sigsdt As Double
Dim lnS As Double, LnSt1 As Double, LnSt2 As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim e As Double
Dim St1 As Double, St2 As Double
Dim CT As Double, CT1 As Double, CT2 As Double
Dim SD As Double, SE As Double
Dim i As Long, j As Long

'Precompute constants

dt = T / N
nudt = (r - div - 0.5 * sig ^ 2#) * dt
sigsdt = sig * Sqr(dt)
lnS = Log(S)

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    LnSt1 = lnS
    LnSt2 = lnS
    
    For i = 1 To N
    
        'For each time step
        
'        e = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
        e = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
        LnSt1 = LnSt1 + nudt + sigsdt * e 'Evolve the stock price
        LnSt2 = LnSt2 + nudt + sigsdt * -e 'Evolve the stock price
        
    Next i
    
    St1 = Exp(LnSt1)
    St2 = Exp(LnSt2)
    CT1 = St1 - K: If CT1 < 0# Then CT1 = 0#
    CT2 = St2 - K: If CT2 < 0# Then CT2 = 0#
    CT = (CT1 + CT2) / 2#
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT + CT * CT
    
Next j

SD = Sqr(sum_CT * sum_CT / M - sum_CT2) * Exp(-2# * r * T) / (M - 1) 'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Call_bMCBS_AVR = sum_CT / M * Exp(-r * T)

End Function

Function European_Call_bMCBS_DCV( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    M As Long) As Double

'European Call Option by Monte Carlo with Black-Scholes and Delta-based Control Variate
'Clewlow/Strickland: Implementing Derivatives Models, page 97
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim nudt As Double, sigsdt As Double, erddt As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim e As Double
Dim St As Double, Stn As Double
Dim CT As Double
Dim SD As Double, SE As Double
Dim beta1 As Double, t1 As Double
Dim cv As Double
Dim delta1 As Double
Dim i As Long, j As Long

'Dim eps As Variant
'eps = Array(0.5391, 0.1692, 0.4583, 0.4164, 0.9223, 0.1597, 0.4011, -0.2382, 1.2152, -0.5506)

'Precompute constants

dt = T / N
nudt = (r - div - 0.5 * sig ^ 2#) * dt
sigsdt = sig * Sqr(dt)
erddt = Exp((r - div) * dt)
beta1 = -1#
'Debug.Print "dt = " & dt & ", nudt = " & nudt & ", sigsdt = " & sigsdt & ", erddt = " & erddt & ", beta1 = " & beta1

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    St = S
    cv = 0#
    
    For i = 1 To N
    
        'For each time step
        
        t1 = CDbl(i - 1) * dt
        delta1 = Black_Scholes_Delta(St, t1, K, T, sig, r, div)
'        Debug.Print "e = " & e & ", St = " & St & ", delta1 = " & delta1 & ", cv = " & cv
'        e = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
        e = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
'        e = eps(i - 1)
        Stn = St * Exp(nudt + sigsdt * e)
        cv = cv + delta1 * (Stn - St * erddt) '* exp(T - (t1 + dt)) 'inflation factor *exp can be omitted
        St = Stn
        
    Next i
    
'    Debug.Print "e = " & e & ", St = " & St & ", delta1 = " & delta1 & ", cv = " & cv
    CT = St - K: If CT < 0# Then CT = 0#
    CT = CT + beta1 * cv
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT + CT * CT
'    Debug.Print "CT = " & CT & ", CT2 = " & CT * CT
    
Next j

SD = Sqr(sum_CT * sum_CT / M - sum_CT2) * Exp(-2# * r * T) / (M - 1) 'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Call_bMCBS_DCV = sum_CT / M * Exp(-r * T)

End Function

Function European_Call_bMCBS_ADCV( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    M As Long) As Double

'European Call Option by Monte Carlo with Black-Scholes and Antithetic and Delta-based Control Variates
'Clewlow/Strickland: Implementing Derivatives Models, page 100
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim nudt As Double, sigsdt As Double, erddt As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim e As Double
Dim St1 As Double, Stn1 As Double
Dim St2 As Double, Stn2 As Double
Dim CT As Double, CT1 As Double, CT2 As Double
Dim SD As Double, SE As Double
Dim beta1 As Double, t1 As Double
Dim cv1 As Double, cv2 As Double
Dim delta1 As Double, delta2 As Double
Dim i As Long, j As Long

'Dim eps As Variant
'eps = Array(0.5391, 0.1692, 0.4583, 0.4164, 0.9223, 0.1597, 0.4011, -0.2382, 1.2152, -0.5506)

'Precompute constants

dt = T / N
nudt = (r - div - 0.5 * sig ^ 2#) * dt
sigsdt = sig * Sqr(dt)
erddt = Exp((r - div) * dt)
beta1 = -1#
'Debug.Print "dt = " & dt & ", nudt = " & nudt & ", sigsdt = " & sigsdt & ", erddt = " & erddt & ", beta1 = " & beta1

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    St1 = S
    St2 = S
    cv1 = 0#
    cv2 = 0#
    
    For i = 1 To N
    
        'For each time step
        
        t1 = CDbl(i - 1) * dt
        delta1 = Black_Scholes_Delta(St1, t1, K, T, sig, r, div)
        delta2 = Black_Scholes_Delta(St2, t1, K, T, sig, r, div)
'        Debug.Print "e = " & e & ", St = " & St & ", delta1 = " & delta1 & ", cv = " & cv
'        e = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
        e = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
'        e = eps(i - 1)
        Stn1 = St1 * Exp(nudt + sigsdt * e)
        Stn2 = St2 * Exp(nudt + sigsdt * -e)
        cv1 = cv1 + delta1 * (Stn1 - St1 * erddt) '* exp(T - (t1 + dt)) 'inflation factor *exp can be omitted
        cv2 = cv2 + delta2 * (Stn2 - St2 * erddt) '* exp(T - (t1 + dt)) 'inflation factor *exp can be omitted
        St1 = Stn1
        St2 = Stn2
        
    Next i
    
'    Debug.Print "e = " & e & ", St = " & St & ", delta1 = " & delta1 & ", cv = " & cv
    CT1 = St1 - K: If CT1 < 0# Then CT1 = 0#
    CT2 = St2 - K: If CT2 < 0# Then CT2 = 0#
    CT = (CT1 + beta1 * cv1 + CT2 + beta1 * cv2) / 2#
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT + CT * CT
'    Debug.Print "CT = " & CT & ", CT2 = " & CT * CT
    
Next j

SD = Sqr(sum_CT * sum_CT / M - sum_CT2) * Exp(-2# * r * T) / (M - 1) 'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Call_bMCBS_ADCV = sum_CT / M * Exp(-r * T)

End Function

Function European_Call_bMCBS_ADGCV( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    N As Long, _
    M As Long) As Double

'European Call Option by Monte Carlo with Black-Scholes and Antithetic, Delta-
'and Gamma-based Control Variates
'Clewlow/Strickland: Implementing Derivatives Models, page 102
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim nudt As Double, sigsdt As Double
Dim erddt As Double, egamma As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim e As Double
Dim St1 As Double, Stn1 As Double
Dim St2 As Double, Stn2 As Double
Dim CT As Double, CT1 As Double, CT2 As Double
Dim SD As Double, SE As Double
Dim beta1 As Double, beta2 As Double, t1 As Double
Dim cv1 As Double, cv2 As Double
Dim delta1 As Double, delta2 As Double
Dim gamma1 As Double, gamma2 As Double
Dim i As Long, j As Long

'Dim eps As Variant
'eps = Array(0.5391, 0.1692, 0.4583, 0.4164, 0.9223, 0.1597, 0.4011, -0.2382, 1.2152, -0.5506)

'Precompute constants

dt = T / N
nudt = (r - div - 0.5 * sig ^ 2#) * dt
sigsdt = sig * Sqr(dt)
erddt = Exp((r - div) * dt)
egamma = Exp((2# * (r - div) + sig * sig) * dt) - 2# * erddt + 1#
beta1 = -1#
beta2 = -0.5
'Debug.Print "dt = " & dt & ", nudt = " & nudt & ", sigsdt = " & sigsdt & ", erddt = " & erddt & ", beta1 = " & beta1

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    St1 = S
    St2 = S
    cv1 = 0#
    cv2 = 0#
    
    For i = 1 To N
    
        'For each time step
        
        'Compute hedge sensitivities
        t1 = CDbl(i - 1) * dt
        delta1 = Black_Scholes_Delta(St1, t1, K, T, sig, r, div)
        delta2 = Black_Scholes_Delta(St2, t1, K, T, sig, r, div)
        gamma1 = Black_Scholes_Gamma(St1, t1, K, T, sig, r, div)
        gamma2 = Black_Scholes_Gamma(St2, t1, K, T, sig, r, div)
        
        'Evolve asset prices
'        Debug.Print "e = " & e & ", St = " & St & ", delta1 = " & delta1 & ", cv = " & cv
'        e = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
        e = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
'        e = eps(i - 1)
        Stn1 = St1 * Exp(nudt + sigsdt * e)
        Stn2 = St2 * Exp(nudt + sigsdt * -e)
        
        'Accumulate control variates
        cv1 = cv1 + delta1 * (Stn1 - St1 * erddt) + _
                    delta2 * (Stn2 - St2 * erddt)
        cv2 = cv2 + gamma1 * ((Stn1 - St1) ^ 2 - St1 ^ 2 * egamma) + _
                    gamma2 * ((Stn2 - St2) ^ 2 - St2 ^ 2 * egamma)
        St1 = Stn1
        St2 = Stn2
        
    Next i
    
'    Debug.Print "e = " & e & ", St = " & St & ", delta1 = " & delta1 & ", cv = " & cv
    CT1 = St1 - K: If CT1 < 0# Then CT1 = 0#
    CT2 = St2 - K: If CT2 < 0# Then CT2 = 0#
    CT = (CT1 + CT2 + beta1 * cv1 + beta2 * cv2) / 2#
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT + CT * CT
'    Debug.Print "CT = " & CT & ", CT2 = " & CT * CT
    
Next j

SD = Sqr(sum_CT * sum_CT / M - sum_CT2) * Exp(-2# * r * T) / (M - 1) 'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Call_bMCBS_ADGCV = sum_CT / M * Exp(-r * T)

End Function

Function European_Spread_bMCBS( _
    K As Double, _
    T As Double, _
    S1 As Double, _
    S2 As Double, _
    sig1 As Double, _
    sig2 As Double, _
    div1 As Double, _
    div2 As Double, _
    rho As Double, _
    r As Double, _
    N As Long, _
    M As Long) As Double

'European Spread Option by Monte Carlo with Black-Scholes
'Clewlow/Strickland: Implementing Derivatives Models, page 110
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim nu1dt As Double, nu2dt As Double
Dim sig1sdt As Double, sig2sdt As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim e1 As Double, e2 As Double
Dim z1 As Double, z2 As Double
Dim St1 As Double, St2 As Double
Dim CT As Double
Dim SD As Double, SE As Double
Dim srho As Double
Dim i As Long, j As Long

'Precompute constants

dt = T / N
nu1dt = (r - div1 - 0.5 * sig1 ^ 2#) * dt
nu2dt = (r - div2 - 0.5 * sig2 ^ 2#) * dt
sig1sdt = sig1 * Sqr(dt)
sig2sdt = sig2 * Sqr(dt)
srho = Sqr(1# - rho ^ 2#)

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    St1 = S1
    St2 = S2
    
    For i = 1 To N
    
        'For each time step
        
        e1 = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
        e2 = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
'        e1 = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
'            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
'        e2 = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
'            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
        z1 = e1
        z2 = rho * e1 + srho * e2
        St1 = St1 * Exp(nu1dt + sig1sdt * z1)
        St2 = St2 * Exp(nu2dt + sig2sdt * z2)
        
    Next i
    
    CT = St1 - St2 - K: If CT < 0# Then CT = 0#
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT + CT * CT
    
Next j

SD = Sqr(sum_CT * sum_CT / M - sum_CT2) * Exp(-2# * r * T) / (M - 1) 'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Spread_bMCBS = sum_CT / M * Exp(-r * T)

End Function

Function European_Spread_bMCBS_SV( _
    K As Double, _
    T As Double, _
    S1 As Double, _
    S2 As Double, _
    sig1 As Double, _
    sig2 As Double, _
    div1 As Double, _
    div2 As Double, _
    alpha1 As Double, _
    alpha2 As Double, _
    Vbar1 As Double, _
    Vbar2 As Double, _
    xi1 As Double, _
    xi2 As Double, _
    rhoz As Variant, _
    r As Double, _
    N As Long, _
    M As Long) As Double

'European Spread Option by Monte Carlo with Black-Scholes and Stochastic Volatilities
'Clewlow/Strickland: Implementing Derivatives Models, page 113
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 14-Apr-2023 PB V1.0

Dim dt As Double
Dim xi1sdt As Double, xi2sdt As Double
Dim alpha1dt As Double, alpha2dt As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim LnS1 As Double, LnS2 As Double
Dim LnSt1 As Double, LnSt2 As Double
Dim v1 As Double, v2 As Double
Dim vt1 As Double, vt2 As Double
Dim z1 As Double, z2 As Double
Dim St1 As Double, St2 As Double
Dim CT As Double
Dim SD As Double, SE As Double
Dim sdt As Double
Dim i As Long, j As Long
Dim z As Variant

'Precompute constants

dt = T / N
alpha1dt = alpha1 * dt
alpha2dt = alpha2 * dt
xi1sdt = xi1 * Sqr(dt)
xi2sdt = xi2 * Sqr(dt)
sdt = Sqr(dt)
LnS1 = Log(S1)
LnS2 = Log(S2)
v1 = sig1 * sig1
v2 = sig2 * sig2

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    LnSt1 = LnS1
    LnSt2 = LnS2
    vt1 = v1
    vt2 = v2
    
    'Generate correlated normals
    z = RandCorr(N, rhoz)
    
    For i = 1 To N 'For each time step
                
        'Simulate variances first
        
        vt1 = vt1 + alpha1dt * (Vbar1 - vt1) + xi1sdt * Sqr(vt1) * z(i, 3)
        vt2 = vt2 + alpha2dt * (Vbar2 - vt2) + xi2sdt * Sqr(vt2) * z(i, 4)
        
        'Simulate asset prices
        
        LnSt1 = LnSt1 + (r - div1 - vt1 / 2#) * dt + Sqr(vt1) * sdt * z(i, 1)
        LnSt2 = LnSt2 + (r - div2 - vt2 / 2#) * dt + Sqr(vt2) * sdt * z(i, 2)
        
    Next i
    
    St1 = Exp(LnSt1)
    St2 = Exp(LnSt2)
    
    CT = St1 - St2 - K: If CT < 0# Then CT = 0#
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT + CT * CT
    
Next j

SD = Sqr(sum_CT * sum_CT / M - sum_CT2) * Exp(-2# * r * T) / (M - 1) 'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Spread_bMCBS_SV = sum_CT / M * Exp(-r * T)

End Function

Function European_Down_and_Out_Call_bMCBS( _
    K As Double, _
    T As Double, _
    S As Double, _
    sig As Double, _
    r As Double, _
    div As Double, _
    H As Long, _
    N As Long, _
    M As Long) As Double

'European Down and Out Call Option by Monte Carlo with Black-Scholes
'Clewlow/Strickland: Implementing Derivatives Models, page 116
'Source (EN): http://www.sulprobil.de/options_en/
'Source (DE): http://www.berndplumhoff.de/options_de/
'Excel VBA implementation by Bernd Plumhoff 02-Jan-2022 PB V1.0

Dim dt As Double
Dim nudt As Double, sigsdt As Double
Dim lnS As Double, lnSt As Double
Dim sum_CT As Double, sum_CT2 As Double
Dim e As Double
Dim St As Double, CT As Double
Dim SD As Double, SE As Double
Dim i As Long, j As Long
Dim bBarrierCrossed As Boolean

#If MODULE_TEST Then
    e = Rnd(-1)
    Randomize 1 'maybe even additional parameter to function
#End If

'Precompute constants

dt = T / N
nudt = (r - div - sig * sig / 2#) * dt
sigsdt = sig * Sqr(dt)

sum_CT = 0#
sum_CT2 = 0#

For j = 1 To M

    'For each simulation
    
    St = S
    bBarrierCrossed = False
    
    For i = 1 To N
    
        'For each time step
        
'        e = Application.WorksheetFunction.NormSInv(Rnd()) 'Standard normal sample
        e = Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + Rnd() + _
            Rnd() + Rnd() + Rnd() + Rnd() - 6# 'Standard normal sample
        St = St * Exp(nudt + sigsdt * e) 'Evolve the stock price
        If St <= H Then
            bBarrierCrossed = True
            Exit For
        End If
        
    Next i
    
    If bBarrierCrossed Then
        CT = 0#
    Else
        CT = St - K
        If CT < 0# Then CT = 0#
    End If
    
    sum_CT = sum_CT + CT
    sum_CT2 = sum_CT + CT * CT
    
Next j

SD = Sqr(Abs(sum_CT * sum_CT / M - sum_CT2)) * Exp(-2# * r * T) / (M - 1) 'Standard deviation
SE = SD / Sqr(M) 'Standard error
European_Down_and_Out_Call_bMCBS = sum_CT / M * Exp(-r * T)

End Function

Download

Bitte den Haftungsausschluss im Impressum beachten.

Clewlow_Strickland_Implementing_Derivatives_Models.xlsm [96 KB Excel Datei, ohne jegliche Gewährleistung]