Wie? O! Dies π
Macht ernstlich so vielen viele Müh’!
Lernt immerhin, Jünglinge, leichte Verselein
Wie so zum Beispiel dies dürfte zu merken sein! [Merkvers für π - Buchstabenanzahl der Wörter, Christian Morgenstern]
Abstract
Wie viele Dezimalstellen der Kreiszahl π werden für die Praxis gebraucht?
Der Hamburger Mathematikprofessor Hermann Schubert zeigte 1889, wieviel Stellen nicht mehr benötigt werden: Man stelle sich eine Kugel vor, in deren Mitte die Erde liegt. Der Radius sei so groß wie die Entfernung der Erde vom Sirius: 8,8 Lichtjahre. Diese Kugel sei mit Mikroben gefüllt, von denen viele Millionen in einen Kubikmillimeter passen. Nun fädele man alle Mikroben in dieser Kugel an einem straffen Faden auf und lasse zwischen je zwei Mikroben einen Platz von 8,8 Lichtjahren. Diesen Faden nehme man als Durchmesser eines Kreises. Multipliziert man diese Länge mit π (auf 100 Dezimalstellen genau), so weicht das Ergebnis vom exakten Umfang des Kreises weniger als ein Millionstel Millimeter ab.
Dieses Beispiel zeigt, daß die Berechnung von π auf 100 Stellen oder mehr vollkommen nutzlos ist.
Warum wird dann versucht, π auf immer mehr Stellen zu berechnen?
In jüngster Zeit möchte man erfahren, ob die Folge der Dezimalziffern gewissen Gesetzen genügt oder nicht. Auch ist nicht bekannt, wie häufig alle Ziffern in der Dezimaldarstellung vorkommen.
Die Berechnung der Kreiszahl π
Bis in die Mitte des 17. Jahrhunderts wurde π nach der Methode des Archimedes berechnet.
Er berechnete die Fläche des Einheitskreises näherungsweise mit Polygonflächen.
James Gregory entdeckte 1671 die Potenzreihe 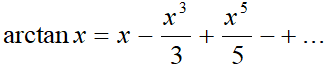 für -1 <= x <= 1.
für -1 <= x <= 1.
Mit dieser Reihenentwicklung und der Gleichung
 wird π in der jüngsten Zeit berechnet.
wird π in der jüngsten Zeit berechnet.

Eine Tabelle zur Geschichte der Näherungen von π
| Jahr | Stellen | Name |
|---|---|---|
| -225 | 2 | Archimedes |
| 1579 | 9 | Viete |
| 1593 | 15 | Roomen |
| 1610 | 35 | Ceulen |
| 1699 | 72 | Sharp |
| 1719 | 112 | de Lagny |
| 1794 | 140 | von Vega |
| 1794 | 200 | Dahse |
| 1873 | 527 | Shanks |
| 1945-48 | 808 | Smith & Wrench |
| 1949 | 2.037 | Reitwiesner |
| 1954-55 | 3.089 | Nicholson & Jeenel |
| 1958 | 10.000 | Genuys |
| 1959 | 16.167 | Genuys |
| 1961 | 100.000 | Shanks & Wrench |
| 1966 | 250.000 | Gilloud & Fillatoire |
| 1967 | 500.000 | Gilloud & Dichampt |
Exkurs: Die Berechnung der Eulerschen Zahl e
e = 2,718281828459045… - Merkhilfe: Die Universität Dresden wurde am 2. Juli 1828 gegründet. Das Jahr wird verdoppelt, danach folgen die Innenwinkel eines Geodreiecks
Zur Berechnung der Eulerschen Zahl e verwendet man die bekannte Summenformel 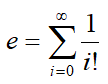 .
.
Also ist 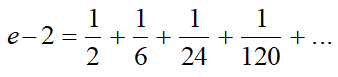 .
.
Jede reelle Zahl 0 <= x < 1 kann man darstellen als (möglicherweise unendlichen)
“variablen Basis”-Bruch 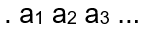 ,
wobei für alle i gilt: 0 <= a(i) < 1. Die dargestellte Zahl ist
,
wobei für alle i gilt: 0 <= a(i) < 1. Die dargestellte Zahl ist 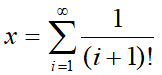 .
.
Die reelle Zahl e - 2 wird demnach dargestellt durch den unendlichen Bruch .111… . Das Problem der Berechnung von e reduziert sich damit auf die Umwandlung der obigen Darstellung in Dezimaldarstellung. Je mehr Stellen man für die Dezimaldarstellung ermitteln will, desto “länger” muss der “variable Basis”-Bruch sein, den man umwandelt.
Beispiel: Berechnung von e auf 1000 Stellen.
Ab welchem Index n kann man den Reihenrest vernachlässigen?
Sei y(n) die (n+1)-te Partialsumme der unendlichen Reihe 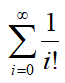 .
Es gilt:
.
Es gilt: 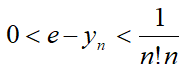 .
(Quelle: Fichtenholz Band I, Nr. 37)
.
(Quelle: Fichtenholz Band I, Nr. 37)
Für dieses Beispiel muss 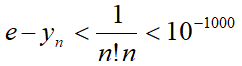 gelten.
Dafür wähle man n = 500.
gelten.
Dafür wähle man n = 500.
Literatur
Nievergelt, Farrer, Reingold: Computer Approaches to Mathematical Problems; Prentice Hall, Inc. 1974, p. 191 + 192, p. 198 - 202.
Ullman: Fundamental Concepts of Programming Systems; Addison-Wesley Publishing Company 1976, p. 48 + 49.
Fichtenholz; Differential- und Integralrechnung Band I + II; VEB Deutscher Verlag der Wissenschaften 1981, Nr. 37 + 50 + 410.
Appendix - pi Programmcode
Bitte den Haftungsausschluss im Impressum beachten.
Option Explicit
Const n = 1050
Dim m1 As Integer
Dim m2 As Integer
Dim m3 As Integer
Const z1 = 554
Const z2 = 285
Const z3 = 211
Dim a(n) As Integer
Dim u_b(n) As Integer
Dim c(n) As Integer
Dim d(n) As Integer
Dim p(n) As Integer
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim r As Integer
Dim u As Integer
Dim v As Integer
Dim x As Integer
Dim y As Integer
Sub addiere()
u = 0
For j = n To 0 Step -1
p(j) = p(j) + a(j) + u
u = p(j) \ 10
p(j) = p(j) - 10 * u
Next j
End Sub
Sub subtrahiere()
u = 1
For j = n To 0 Step -1
p(j) = p(j) + 9 - a(j) + u
u = p(j) \ 10
p(j) = p(j) - 10 * u
Next j
End Sub
Sub pi()
' pi auf 1000 Stellen ausgeben
For i = 0 To n
a(i) = 0
u_b(i) = 0
c(i) = 0
d(i) = 0
p(i) = 0
Next i
m1 = 8
m2 = 57
m3 = 239
'Der erste Summand jeder Reihe wird ermittelt
'b(I) = 24 \ 8
u_b(0) = 24 \ 8
p(0) = u_b(0)
c(0) = 8
r = 0 'r enthält immer den Rest der Division
'c(I) = 8\57
For i = 0 To n
a(i) = (10 * r + c(i)) \ m2
r = 10 * r + c(i) - a(i) * m2
Next i
For i = 0 To n
c(i) = a(i)
Next i
addiere
d(0) = 4
r = 0
'd(I) = 4\239
For i = 0 To n
a(i) = (10 * r + d(i)) \ m3
r = 10 * r + d(i) - a(i) * m3
Next i
For i = 0 To n
d(i) = a(i)
Next i
addiere
' Nun wird die Reihe von 24 arctan 1\8 berechnet
v = -1 'Das Vorzeichen des Summanden
m1 = m1 * m1
k = 3
For i = 1 To z1
r = 0
For j = 0 To n
a(j) = (10 * r + u_b(j)) \ m1
r = 10 * r + u_b(j) - a(j) * m1
Next j
For j = 0 To n
u_b(j) = a(j)
Next j
r = 0
For j = 0 To n
a(j) = (10 * r + u_b(j)) \ k
r = 10 * r + u_b(j) - a(j) * k
Next j
If v = 1 Then addiere Else subtrahiere
k = k + 2
v = 0 - v
Next i
' Nun wird die Reihe von 8 arctan 1\57 berechnet
v = -1
m2 = m2 * m2
k = 3
For i = 1 To z2
r = 0
For j = 0 To n
a(j) = (10 * r + c(j)) \ m2
r = 10 * r + c(j) - a(j) * m2
Next j
For j = 0 To n
c(j) = a(j)
Next j
r = 0
For j = 0 To n
a(j) = (10 * r + c(j)) \ k
r = 10 * r + c(j) - a(j) * k
Next j
If v = 1 Then addiere Else subtrahiere
k = k + 2
v = 0 - v
Next i
' Nun wird die Reihe von 4 arctan 1\239 berechnet
v = -1
k = 3
For i = 1 To z3
r = 0
For j = 0 To n
a(j) = (10 * r + d(j)) \ m3
r = 10 * r + d(j) - a(j) * m3
Next j
r = 0
For j = 0 To n
d(j) = (10 * r + d(j)) \ m3
r = 10 * r + a(j) - d(j) * m3
Next j
r = 0
For j = 0 To n
a(j) = (10 * r + d(j)) \ k
r = 10 * r + d(j) - a(j) * k
Next j
If v = 1 Then addiere Else subtrahiere
k = k + 2
v = 0 - v
Next i
x = 1
y = 1
Open ThisWorkbook.Path & "/pi.txt" For Output As #1
Print #1, "Pi = " & p(0) & ".";
For i = 1 To 1000
Print #1, Format(p(i), "&");
x = x + 1
If x > 3 Then
Print #1, " ";
x = 1
End If
y = y + 1
If y > 42 Then
Print #1, " "
Print #1, " ";
y = 1
End If
Next i
Close #1
End Sub
Appendix - pi Ausgabe
Pi = 3.141 592 653 589 793 238 462 643 383 279 502 884 197 169
399 375 105 820 974 944 592 307 816 406 286 208 998 628
034 825 342 117 067 982 148 086 513 282 306 647 093 844
609 550 582 231 725 359 408 128 481 117 450 284 102 701
938 521 105 559 644 622 948 954 930 381 964 428 810 975
665 933 446 128 475 648 233 786 783 165 271 201 909 145
648 566 923 460 348 610 454 326 648 213 393 607 260 249
141 273 724 587 006 606 315 588 174 881 520 920 962 829
254 091 715 364 367 892 590 360 011 330 530 548 820 466
521 384 146 951 941 511 609 433 057 270 365 759 591 953
092 186 117 381 932 611 793 105 118 548 074 462 379 962
749 567 351 885 752 724 891 227 938 183 011 949 129 833
673 362 440 656 643 086 021 394 946 395 224 737 190 702
179 860 943 702 770 539 217 176 293 176 752 384 674 818
467 669 405 132 000 568 127 145 263 560 827 785 771 342
757 789 609 173 637 178 721 468 440 901 224 953 430 146
549 585 371 050 792 279 689 258 923 542 019 956 112 129
021 960 864 034 418 159 813 629 774 771 309 960 518 707
211 349 999 998 372 978 049 951 059 731 732 816 096 318
595 024 459 455 346 908 302 642 522 308 253 344 685 035
261 931 188 171 010 003 137 838 752 886 587 533 208 381
420 617 177 669 147 303 598 253 490 428 755 468 731 159
562 863 882 353 787 593 751 957 781 857 780 532 171 226
806 613 001 927 876 611 195 909 216 420 198 9
Appendix - e Programmcode
Bitte den Haftungsausschluss im Impressum beachten.
Option Explicit
Sub e()
'e auf 1000 Stellen ausgeben
Dim a(500) As Long
Dim c As Long
Dim d As Long
Dim i As Long
Dim j As Long
Dim x As Integer
Dim y As Integer
Open ThisWorkbook.Path & "/e.txt" For Output As #1
Print #1, "e = 2.";
For i = 1 To 500
a(i) = 1
Next i
For i = 1 To 1000
c = 0
For j = 500 To 1 Step -1
d = 10 * a(j) + c
c = Fix(d / (j + 1))
a(j) = d - c * (j + 1)
Next j
x = x + 1
If x > 3 Then
Print #1, " ";
x = 1
End If
y = y + 1
If y > 42 Then
Print #1, " "
Print #1, " ";
y = 1
End If
Print #1, Format(c, "&");
Next i
Close #1
End Sub
Appendix - e Ausgabe
e = 2.718 281 828 459 045 235 360 287 471 352 662 497 757 247
093 699 959 574 966 967 627 724 076 630 353 547 594 571
382 178 525 166 427 427 466 391 932 003 059 921 817 413
596 629 043 572 900 334 295 260 595 630 738 132 328 627
943 490 763 233 829 880 753 195 251 019 011 573 834 187
930 702 154 089 149 934 884 167 509 244 761 460 668 082
264 800 168 477 411 853 742 345 442 437 107 539 077 744
992 069 551 702 761 838 606 261 331 384 583 000 752 044
933 826 560 297 606 737 113 200 709 328 709 127 443 747
047 230 696 977 209 310 141 692 836 819 025 515 108 657
463 772 111 252 389 784 425 056 953 696 770 785 449 969
967 946 864 454 905 987 931 636 889 230 098 793 127 736
178 215 424 999 229 576 351 482 208 269 895 193 668 033
182 528 869 398 496 465 105 820 939 239 829 488 793 320
362 509 443 117 301 238 197 068 416 140 397 019 837 679
320 683 282 376 464 804 295 311 802 328 782 509 819 455
815 301 756 717 361 332 069 811 250 996 181 881 593 041
690 351 598 888 519 345 807 273 866 738 589 422 879 228
499 892 086 805 825 749 279 610 484 198 444 363 463 244
968 487 560 233 624 827 041 978 623 209 002 160 990 235
304 369 941 849 146 314 093 431 738 143 640 546 253 152
096 183 690 888 707 016 768 396 424 378 140 592 714 563
549 061 303 107 208 510 383 750 510 115 747 704 171 898
610 687 396 965 521 267 154 688 957 035 035 4
Download
Bitte den Haftungsausschluss im Impressum beachten.
pi.xlsm [22 KB Excel Datei, ohne jegliche Gewährleistung]