Abstract
Sie wollen eine Zahl als nicht-negative Linearkombination zweier natürlicher Zahlen darstellen?
Dies kann man mit dem (externer Link!) erweiterten Euklidischen Algorithmus erreichen:
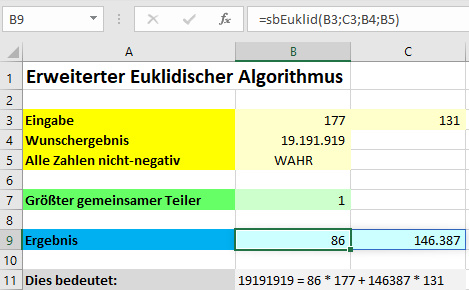
Hinweis: Wenn das Wunschergebnis ein Vielfaches des größten gemeinsamen Teilers der eingegebenen Zahlen ist, dann existiert immer eine ganzzahlige Lösung, aber nicht notwendigerweise eine nicht-negative. Beispiel: Sie können mit den Eingaben 5 und 3 das Wunschergebnis 1 ganzzahlig darstellen, weil 1 der GGT von 5 und 3 ist: 1 = 2 * 5 + (-3) * 3. Aber es geht nicht mit ausschließlich nicht-negativen Faktoren.
Ein weiterer Hinweis: Es können mehrere nicht-negative Lösungen existieren, mit bAllNonNegative = WAHR gibt der u. g. Algorithmus die kleinste Summe der Ausgabewerte zurück. Wenn eine ganzzahlige Lösung existiert, dann gibt es abzählbar viele Lösungen.
Appendix – sbEuklid Programmcode
Bitte den Haftungsausschluss im Impressum beachten.
Die möglichen Fehlercodes des Programms bedeuten:
- #NV! - Es existiert keine Lösung
- #WERT! - bAllNonNegative = WAHR aber nicht alle Eingaben sind nicht-negativ
- #ZAHL! - bAllNonNegative = WAHR aber es existiert keine nicht-negative Lösung
Option Explicit
Function sbEuklid(lInput1 As Long, _
lInput2 As Long, _
Optional lDesiredResult As Long, _
Optional bAllNonNegative As Boolean = False) As Variant
'Extended Euklidean Algorithm which calculates two factors f1 and f2
'so that lDesiredResult = f1 * lInput1 + f2 * lInput2. If lDesiredResult
'is not given, the greatest common divisor (GCD) of lInput1 and lInput2
'will be calculated. If bAllNonNegative is True then we try to achieve a
'non-negative result of all inputs and outputs with minimal Sum(f1+f2).
'Error return values can be:
'xlErrNA - There is no solution
'xlErrValue - bAllNonNegative = True but not all inputs are non-negative
'xlErrNum - bAllNonNegative = True but there is no non-negative solution
'Source (EN): http://www.sulprobil.de/sbeuklid_en/
'Source (DE): http://www.berndplumhoff.de/sbeuklid_de/
'(C) (P) by Bernd Plumhoff 20-May-2024 PB V0.4
Dim lDiv As Long
Dim lGCD As Long
Dim lRest As Long
Dim lT1 As Long
Dim lT2 As Long
Dim vR As Variant
Dim vT As Variant
With Application '.WorksheetFunction 'Test with, release without
lGCD = .Gcd(lInput1, lInput2)
If IsMissing(lDesiredResult) Then lDesiredResult = lGCD
lRest = lDesiredResult Mod lGCD
If lRest <> 0 Then
sbEuklid = CVErr(xlErrNA) 'There is no solution
Else
If bAllNonNegative And (lInput1 < 0 Or lInput2 < 0 Or lDesiredResult < 0) Then
sbEuklid = CVErr(xlErrValue) 'bAllNonNegative but not all inputs are non-negative
Else
'See https://www.arndt-bruenner.de/mathe/scripts/erweitertereuklid.htm
vR = [{1, 0; 0, 1}]
vT = [{0, 1; 1, 0}]
lT1 = lInput1
lT2 = lInput2
Do
lDiv = lT1 \ lT2
lRest = lT1 Mod lT2
lT1 = lT2
lT2 = lRest
vT(2, 2) = -lDiv
vR = .MMult(vR, vT)
Loop While lRest <> 0
vR = .MMult(Array(lDesiredResult \ lGCD, 0), .Transpose(vR))
Debug.Assert lDesiredResult = vR(1) * lInput1 + vR(2) * lInput2 'Just assuring
sbEuklid = vR
If bAllNonNegative Then
If lInput1 > lInput2 Then
lT1 = lDesiredResult \ lInput1 + 1
Do While lT1 > 0
lT1 = lT1 - 1
If (lDesiredResult - lInput1 * lT1) Mod lInput2 = 0 Then GoTo Success1
Loop
GoTo ErrorExit
Success1: vR(1) = lT1
vR(2) = (lDesiredResult - lInput1 * lT1) \ lInput2
Else
lT2 = lDesiredResult \ lInput2 + 1
Do While lT2 > 0
lT2 = lT2 - 1
If (lDesiredResult - lInput2 * lT2) Mod lInput1 = 0 Then GoTo Success2
Loop
GoTo ErrorExit
Success2: vR(2) = lT2
vR(1) = (lDesiredResult - lInput2 * lT2) \ lInput1
End If
sbEuklid = vR
End If
End If
End If
'Debug.Assert lDesiredResult = vR(1) * lInput1 + vR(2) * lInput2 'Just testing
Exit Function
ErrorExit:
sbEuklid = CVErr(xlErrNum)
End With
End Function
Download
Bitte den Haftungsausschluss im Impressum beachten.
sbEuklid.xlsm [25 KB Excel Datei, ohne jegliche Gewährleistung]