“Die ganzen Zahlen hat der liebe Gott gemacht, alles andere ist Menschenwerk.” [Leopold Kronecker]

Abstract

Welche rationale Zahl ist eine gute Näherung von π (3,1415926…)? Geben Sie ein: in Zelle A1 ‘=pi()’, in Zelle B1 den maximal gewünschten Nenner (zum Beispiel 10), und als Matrixformel (mit STRG + SHIFT + ENTER) in den Zellen C1:D1 ‘=sbNRN(A1;B1)’. Als Ergebnis erscheint in C1:D1 22 und 7. Dies bedeutet: 22/7 ist die nächstliegende rationale Zahl (Bruch) zu π mit einem Nenner nicht größer als 10. Mit 1000 in B1 würde man 355/113 erhalten.

Dieser Algorithmus findet nicht immer die nächstliegende rationale Zahl zu einer gegebenen Gleitkommazahl mit einem gewünschten maximalen Nenner und der vordefinierten maximalen Fehlerschranke 1# / (2# * CDbl(lMaxDen) ^ 2#). Die gute Nachricht ist jedoch, dass er dann einen #ZAHL! Fehler zurückgeben würde. In einem solchen Fall geben Sie bitte eine größere individuelle maximale Fehlerschranke vor.

Die ursprüngliche Absicht des Autoren Oliver Aberth bestand in der Unterstützung exakter Berechnungen von Brüchen, zum Beispiel bei der Lösung von linearen Gleichungssystemen mit rationalen Koeffizienten .

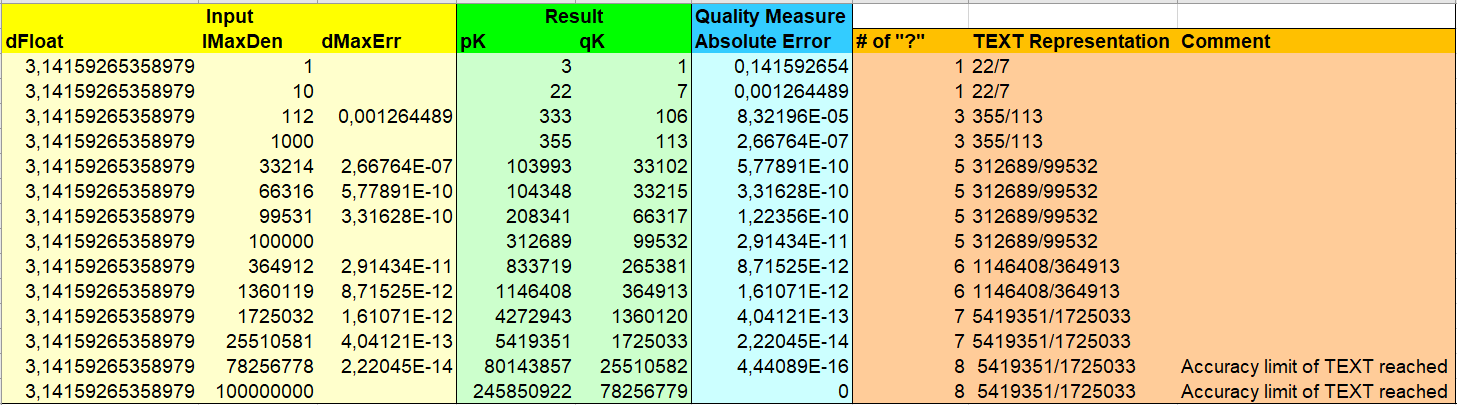
Bemerkung: Die letzte Zeile in der obigen Grafik sagt uns nicht, dass wir den Kreis erfolgreich quadriert haben. Wir haben lediglich (meines) Excel’s Genauigkeitsgrenze erreicht.

Die Bruchdarstellungen der TEXT Funktion wurden zum Vergleich angezeigt.
Beispiel: =TEXT(PI();"?/?") = “22/7”
Microsoft hat diese Darstellung nicht für die 64-Bit Version erweitert. Genauer als PI() = “5419351/1725033” kann nicht gezeigt werden. Genauer wäre mit 64-Bit PI() = “245850922/78256779”, aber dann ist der absolute Fehler ist natürlich längst kleiner als 1e-15.

Eine einfache Beispielanwendung finden Sie unter Anteilsveränderung als Bruch.

Grenzen der Berechnung

Excel kann Dezimalzahlen von -9,99999999999999E+307 bis 9,99999999999999E+307 darstellen. Die 64-Bit Version von Excel kann ganze Zahlen des Typs LongLong von -9223372036854775808 bis 9223372036854775807 darstellen, was in etwa dem Umfang -1E+10 bis 1E+10 entspricht.

Es ist offensichtlich, dass Aberth’s Algorithmus in Excel nicht alle verfügbaren Dezimalzahlen hinreichend genau als Bruch ermitteln kann.

Name

sbNRN - Berechne die nächstliegende rationale Zahl zu einer gegebenen Gleitkommazahl mit einem gegebenen maximalen Nenner

Synopsis

sbNRN(dFloat, lMaxDen, [dMaxErr])

Beschreibung

sbNRN berechnet die nächstliegende rationale Zahl (Bruch) zu einer gegebenen Gleitkommazahl dFloat mit einem maximalen Nenner lMaxDen und einer optionalen maximalen absoluten Fehlerschranke dMaxErr.

Parameter

dFloat - Die Gleitkommazahl für die die nächstliegende rationale Zahl gefunden werden soll

lMaxDen - Die Obergrenze für den Nenner

dMaxErr - Optional - Die Obergrenze für den absoluten Fehler (absolute Differenz zwischen der eingegebenen Gleitkommazahl und der auszugebenden rationalen Zahl)

Literatur

(Externer Link!) Oliver Aberth, A method for exact computation with rational numbers, JCAM, vol 4, no. 4, 1978

Oliver Aberth, Introduction to Precise Numerical Methods, ISBN 0-12-373859-8

(Externer Link!) George Chrystal, Algebra an Elementary Text-Book, Part II, Chapter 32, p. 423 ff, 1900

(Externer Link!) Peter Henrici, A Subroutine for Computations with Rational Numbers, JACM, vol 3, no. 1, 1956

Siehe auch

Exakte Rechnung mit rationalen Zahlen

Exkurs

Falls Sie lediglich die Relation zur Zehnerpotenz benötigen, können Sie die folgende Formel verwenden: =WENNFEHLER(–A2*10^(LÄNGE(–A2)-SUCHEN(",";–A2))&":"&10^(LÄNGE(–A2)-SUCHEN(",";–A2));–A2&":1"):

Appendix – Programmcode sbNRN

Bitte den Haftungsausschluss im Impressum beachten.

Option Explicit

#If Win64 Then
Function sbNRN(dFloat As Double, lMaxDen As LongLong, _
               Optional dMaxErr As Double = -1#) As Variant
#Else
Function sbNRN(dFloat As Double, lMaxDen As Long, _
               Optional dMaxErr As Double = -1#) As Variant
#End If
'Computes nearest rational number to dFloat with a maximal denominator
'lMaxDen and a maximal absolute error dMaxErr and returns result as a
'variant Nominator / Denominator.
'See: Oliver Aberth, A method for exact computation with rational numbers,
'     JCAM, vol 4, no. 4, 1978
'Source (EN): http://www.sulprobil.de/sbnrn_en/
'Source (DE): http://www.berndplumhoff.de/sbnrn_de/
'Bernd Plumhoff V1.21 09-Oct-2020

Dim dB As Double
#If Win64 Then
Dim lA As LongLong, lSgn As LongLong
Dim lP1 As LongLong, lP2 As LongLong, lP3 As LongLong
Dim lQ1 As LongLong, lQ2 As LongLong, lQ3 As LongLong
#Else
Dim lA As Long, lSgn As Long
Dim lP1 As Long, lP2 As Long, lP3 As Long
Dim lQ1 As Long, lQ2 As Long, lQ3 As Long
#End If

If dMaxErr = -1# Then dMaxErr = 1# / (2# * CDbl(lMaxDen) ^ 2#)
lSgn = Sgn(dFloat): dB = Abs(dFloat)
lP1 = 0: lP2 = 1: lQ1 = 1: lQ2 = 0

Do While lMaxDen > lQ2
    lA = Int(dB)
    lP3 = lA * lP2 + lP1: lQ3 = lA * lQ2 + lQ1
#If Win64 Then
    If Abs(dB - CDbl(lA)) < 1# / CLngLng("9223372036854775807") Then
#Else
    If Abs(dB - CDbl(lA)) < 1# / 2147483647# Then
#End If
        Exit Do
    End If
    dB = 1# / (dB - CDbl(lA))
    lP1 = lP2: lP2 = lP3: lQ1 = lQ2: lQ2 = lQ3
Loop

If lQ3 > lMaxDen Then
    lQ3 = lQ2: lP3 = lP2
    If lQ2 > lMaxDen Then
        lQ3 = lQ1: lP3 = lP1
    End If
End If

'If absolute error exceeds 1/2Q^2 then Aberth's lemma p. 286 might not apply.
'But the user can override this and check the result himself.
If Abs(dFloat - lSgn * lP3 / lQ3) > dMaxErr Then
    sbNRN = CVErr(xlErrNum)
Else
    sbNRN = Array(lSgn * lP3, lQ3)
End If

End Function

Download

Bitte den Haftungsausschluss im Impressum beachten.

sbNRN.xlsm [81 KB Excel Datei, ohne jegliche Gewährleistung]