Abstract
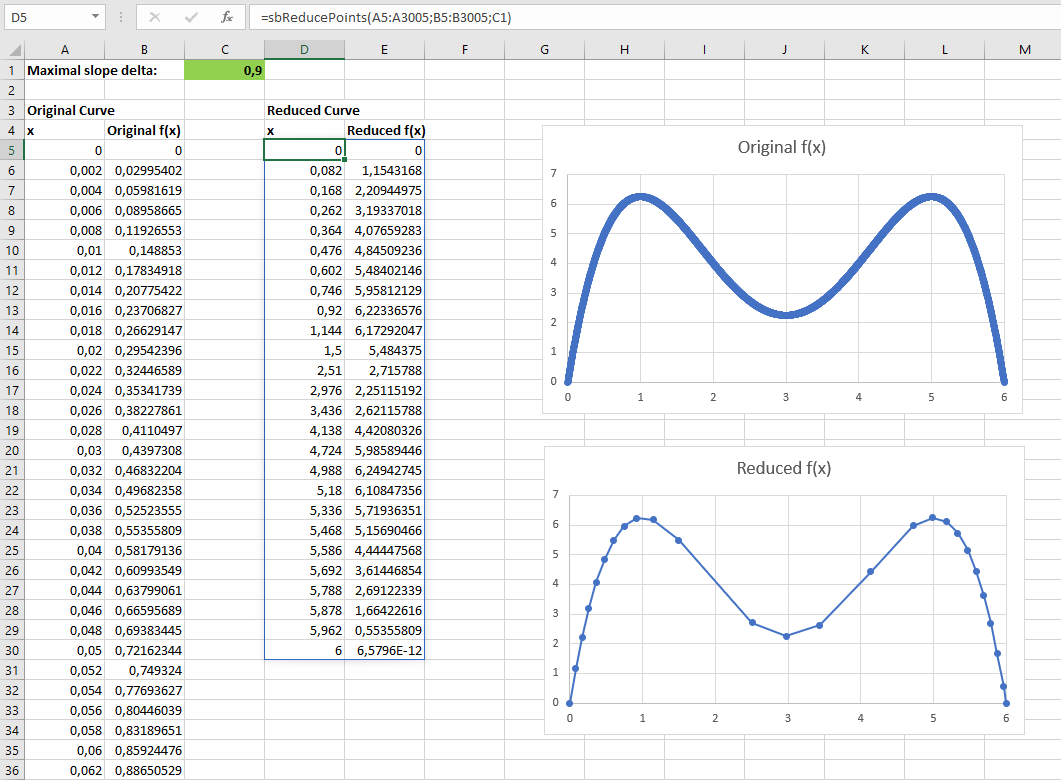
Falls Sie die Anzahl von Kurvenpunkten auf solche mit signifikanter Steigungsänderung reduzieren möchten:
Literatur
Falls dieser einfache Ansatz der Steigungsänderung nicht ausreicht, empfiehlt sich der (externer Link!) Douglas-Peucker-Algorithmus.
Appendix sbReducePoints Code
Bitte den Haftungsausschluss im Impressum beachten.
Option Explicit
Function sbReducePoints(rX As Range, rY As Range, _
Optional dMaxSlopeDelta As Double = 0.001) As Variant
'sbReducePoints eliminates points from a given set
'in case the slopes between these points do not differ
'too much.
'Source (EN): http://www.sulprobil.de/sbreducepoints_en/
'Source (DE): http://www.berndplumhoff.de/sbreducepoints_de/
'(C) (P) by Bernd Plumhoff 29-Mar-2023 PB V0.1
Dim bNewSlope As Boolean
Dim dSlope12 As Double
Dim dSlope13 As Double
Dim dSlope23 As Double
Dim i As Long
Dim k As Long
Dim lcount As Long
With Application.WorksheetFunction
lcount = rX.Rows.Count
If rX.Columns.Count > lcount Then
lcount = rX.Columns.Count
End If
ReDim dX(1 To lcount) As Double
ReDim dY(1 To lcount) As Double
'read data row-wise or column-wise
If rX.Rows.Count > rX.Columns.Count Then
For i = 1 To lcount
dX(i) = rX.Cells(i, 1)
dY(i) = rY.Cells(i, 1)
Next i
Else
For i = 1 To lcount
dX(i) = rX.Cells(1, i)
dY(i) = rY.Cells(1, i)
Next i
End If
ReDim vR(1 To 2, 1 To lcount) As Variant
vR(1, 1) = dX(1)
vR(2, 1) = dY(1)
vR(1, 2) = dX(2)
vR(2, 2) = dY(2)
k = 2
bNewSlope = True
For i = 3 To lcount
If bNewSlope Then dSlope12 = (vR(2, k) - vR(2, k - 1)) / (vR(1, k) - vR(1, k - 1))
dSlope13 = (dY(i) - vR(2, k - 1)) / (dX(i) - vR(1, k - 1))
dSlope23 = (dY(i) - vR(2, k)) / (dX(i) - vR(1, k))
If Abs(dSlope13 - dSlope12) > dMaxSlopeDelta Or _
Abs(dSlope13 - dSlope23) > dMaxSlopeDelta Then
k = k + 1
bNewSlope = True
Else
bNewSlope = False
End If
vR(1, k) = dX(i)
vR(2, k) = dY(i)
Next i
ReDim Preserve vR(1 To 2, 1 To k) As Variant
If rX.Rows.Count > rX.Columns.Count Then
sbReducePoints = .Transpose(vR)
Else
sbReducePoints = vR
End If
End With
End Function
Bitte den Haftungsausschluss im Impressum beachten.
sbReducePoints.xlsm [192 KB Excel Datei, ohne jegliche Gewährleistung]